2023 年 7 月做题记录

2023-07-04

题解/做题记录

20k 词

前言

会在题目名称后给每道题目一个标记，标 ! 的是我认为非常好的 CNOI-Style 的题，标 * 的是 Ad-hoc 或构造或结论题，标 + 的是比较有意思的思维题。根据牛牛程度会增减数量。

CF1137C Museums Tour [!]

$\verb|tags: 图论, Tarjan, 拓扑排序|$

建分层图，然后缩点，对于每个强连通分量求出其中有多少个地方。

然后直接拓扑排序求最长路就是答案。

问题在于为什么同一天不会被重复统计。
发现天数是循环的，也就是说如果某个城市第 $x$ 天和第 $x + y$ 天不在同一个强连通分量里，且能从第 $x$ 天到达第 $x + y$ 天，那一定能从第 $x + y$ 天到达第 $x + 2y$ 天，以此类推，一定能到达 $(x + dy) \bmod d = x$ 天，所以 $x$ 和 $x + y$ 一定在同一个强连通分量里。

CF1137E Train Car Selection [!!]

$\verb|tags: 计算几何|$

首先将下标和值看成二维平面上一个点，那么如果存在 $(i, a _ i), (j, a _ j)$ 满足 $i < j, a _ i < a _ j$ ，因为每次添加的直线的斜率和截距都是正的，所以 $j$ 永远不会成为答案。

另外，如果三个点 $(i, a _ i), (j, a _ j), (k, a _ k)$ ，满足 $i < j < k$ 且 $(j, a _ j)$ 在另外两点连成的直线的上方， $j$ 也一定不会成为答案。

证明：

设添加的直线为 $ux + v$ ，则需要满足 $a _ j + uj + v \le a _ k + uk + v$ 。

即： $a _ j - a _ k \le u(k - j)$ ，即 $u \ge \dfrac{a _ j - a _ k}{k - j}$ 。

另外， $a _ j + uj + v < a _ i + ui + v \Rightarrow u < \dfrac{a _ i - a _ j}{j - i}$ 。

然而 $\dfrac{a _ j - a _ k}{k - j} > \dfrac{a _ i - a _ j}{j - i}$ ，故 $(j, a _ j)$ 永远无法成为最小值。

所以我们只要动态维护下凸壳的纵坐标单调下降部分即可。

对于 1 操作：将维护的集合重置为第一个数，纵坐标为 $0$ 。
对于 2 操作：用添加的第一个数不断从集合末尾弹出元素。
对于 3 操作：维护一个全局标记，然后不断弹出集合末尾不符合要求的元素。并且在 1 操作中清空标记，2 操作中插入点坐标为 $(x, -kx - b)$ 。

注意一些细节问题，然后就做完了。

ARC110F Esoswap [*++]

$\verb|tags: 构造|$

很妙的一道题。

首先，如果 $P _ i = A \neq 0$ ，如果只操作 $i$ ，则 $A$ 不可能回到 $i$ 。
原因显然，第一次操作使得 $P _ {i + A} = A$ ，然后后面的操作都不会动这个点，除非 $P _ i = A$ ，这显然是矛盾的。

于是就有了下一个结论：对一个点操作至多 $n - 1$ 次后其值一定会变为 $0$ 。

进一步，对于 $0$ 前面那一位，一直对它操作，在它变成 $0$ 前一步，它一定会变成 $1$ ，再操作一次这两个数就变成了 $0, 1$ 。

然后再对这两个数前面的那个数操作，变化过程就是这样： $(2, 0, 1) \to (1, 0, 2) \to (0, 1, 2)$ 。

于是我们可以发现，一直循环这个过程可以使序列变成 $(0, 1, 2, 3, 4, \ldots)$ ，证明很简单，这里不再赘述。

于是我们只要从 $n - 1$ 开始往前枚举，对每个位置都操作 $n - 1$ 次即可排序成功。

SCOI2015 小凸玩密室 [!!]

$\verb|tags: 图论, 树, DP|$

很不错的一道题。

考虑 $u$ 这棵子树，假设 $u$ 已经点亮，要点亮这棵子树，怎么求最优解。

我们发现点亮一棵子树时最后点亮的点一定是叶子，于是我们依此设计 DP 状态： $f _ {u, i}$ 表示点亮 $u$ 这棵子树， $u$ 已经被点亮，最后点亮叶子 $i$ 的最少花费。

设 $ls _ u$ 为 $u$ 的左儿子， $rs _ u$ 为 $u$ 的右儿子， $dis(u, v)$ 表示 $u, v$ 两点间的距离，则转移方程为：

f _ {u, i} = \min\left(d(u, rs _ u) a _ {rs _ u} + f _ {rs _ u, j} + d(j, ls _ u) a _ {ls _ u} + f _ {ls _ u, i}\right)

其中叶子 $i$ 在 $ls _ u$ 的子树中。叶子 $i$ 在 $rs _ u$ 的子树中同理。

我们发现 $d(j, ls _ u) = d(j, u) + d(ls _ u, u)$ ，于是我们可以把转移方程拆成两部分，然后预处理一下，获得每个子树 $O(\text{叶子个数})$ 的复杂度。由于是完全二叉树，所以每个子树的叶子个数之和是 $O(n \log n)$ 的。

但是这样只能得到最先点亮根的答案。

考虑点亮别的点怎么办，如果点亮的是 $u$ ，则 $u$ 的答案依然是 $f _ u$ ，然后会走到他的父亲，此时合并两棵子树，另一棵子树答案已经求出，中间的贡献可以简单计算得到，然后一直跳到根，只会跳 $O(\log n)$ 次，看起来很对，但是发现合并答案涉及到叶子个数，所以每次计算答案依然是 $O(n)$ 的。

但是我们发现没必要分开来计算，可以一起计算。具体地，设 $g _ {u, i}$ 表示点亮 $u$ 这棵子树， $u$ 需要被点亮，最后点亮叶子 $i$ 的最小花费。可以得到转移方程：

g _ {u, i} = \min\left(g _ {rs _ u, j} + d(j, u) a _ u + d(u, ls _ u) a _ {ls _ u} + f _ {ls _ u, i}\right)

这里 $i$ 在 $ls _ u$ 的子树中，在 $rs _ u$ 的子树中同理。

最后答案就是 $g _ 1$ ，总时间复杂度 $O(n \log n)$ 。

AGC047E Product Simulation [***+++]

$\verb|tags: 造计算机|$

非常有意思的造计算机题！

目前最优解，次数为 $2938$ ，内存单元个数为 $96$ 。

首先，如果 $a _ 0 = a _ 1 = 0$ ，那么无论如何无法构造出非 $0$ 的数，所以怎么做都是合法的。

考虑竖式乘法，第一步是将两个数转化为二进制，然后把每一位存下来。
我们需要搞出所有 $2 ^ i$ ，那么一种朴素的想法就是先获得 $1$ ，然后不断乘 $2$ （即两个相同的数相加）。
获得 $1$ 的方法是： $a _ 3 \gets a _ 0 + a _ 1, a _ 3 \gets [a _ 4 < a _ 3]$ ，这样就能使 $a _ 3 = 1$ 。然后就可以求出所有 $2 ^ i$ ，用若干内存单元存下来。

add(3, 0, 1);
cmp(3, 4, 3);
for (int i = 1; i <= 29; i++) add(3 + i, 3 + i - 1, 3 + i - 1);
// for each i in 3 ~ 32: 2 ^ {i - 3}

接下来考虑从高位到低位求。具体来说，设当前是第 $i$ 位，我们用一个数记录只考虑当前已经求得值的几位的结果，然后将它与 $2 ^ i$ 相加，如果 $\le a _ 0$ ，则 $a _ 0$ 这一位为 $1$ ，否则为 $0$ 。由于没有 $\le$ 操作，我们先让 $a _ 0 \gets a _ 0 + 1$ 。

// 93: temp value
// 94: temp digit
add(0, 0, 3);
for (int i = 29; i >= 0; i--) {
    add(94, 93, 3 + i);
    cmp(94, 94, 0);
    add(32 + i + 1, 32 + i + 1, 94);
    for (int j = 1; j <= i; j++) add(94, 94, 94);
    add(93, 93, 94);
}

对 $a _ 1$ 的拆分相同。

然后考虑竖式乘法，我们直接枚举没一位，然后计算这两位相乘的结果，因为是二进制，所以结果就是按位与的结果。具体实现是：设这两位分别为 $x, y$ ，分别为第 $i, j$ 位，则令 $z \gets x + y, z \gets [1 < z]$ ，然后再乘上 $2 ^ {i + j}$ （即重复 $\times 2$ 操作 $i + j$ 遍）即可。

for (int i = 0; i <= 58; i++) {
    cmp(93, 93, 95); // a[95] = 0，使用这种方法清 0 一个内存单元。
    for (int j = 0; j <= min(29, i); j++) {
        if (i - j > 29) continue;
        add(94, 32 + i - j + 1, 62 + j + 1);
        cmp(94, 3, 94);
        add(93, 93, 94);
    }
    for (int j = 1; j <= i; j++) add(93, 93, 93);
    add(2, 2, 93);
}

完整代码：

记录：Submission #43274995。

// Think twice, code once.
#include <tuple>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
// #define DEBUG
using namespace std;

int a[1005];
vector<tuple<char, int, int, int>> ans;

void cmp(int i, int j, int k) {ans.emplace_back('<', j, k, i); a[i] = a[j] < a[k]; return ;}
void add(int i, int j, int k) {ans.emplace_back('+', j, k, i); a[i] = a[j] + a[k]; return ;}

int main() {
#ifdef DEBUG
	scanf("%d%d", &a[0], &a[1]);
#endif
	add(3, 0, 1);
	cmp(3, 4, 3);
	add(0, 0, 3), add(1, 1, 3);
	for (int i = 1; i <= 29; i++) add(3 + i, 3 + i - 1, 3 + i - 1);
	// for each i in 3 ~ 32: 2 ^ {i - 3}
	// 93: temp value
	// 94: temp digit
	// 95: zero
	for (int i = 29; i >= 0; i--) {
		add(94, 93, 3 + i);
		cmp(94, 94, 0);
		add(32 + i + 1, 32 + i + 1, 94);
		for (int j = 1; j <= i; j++) add(94, 94, 94);
		add(93, 93, 94);
	}
	// for each i in 33 ~ 62: x's (i - 33)th digit in binary.
	cmp(93, 93, 95);
	for (int i = 29; i >= 0; i--) {
		add(94, 93, 3 + i);
		cmp(94, 94, 1);
		add(62 + i + 1, 62 + i + 1, 94);
		for (int j = 1; j <= i; j++) add(94, 94, 94);
		add(93, 93, 94);
	}
	// for each i in 63 ~ 92: y's (i - 63)th digit in binary.
	for (int i = 0; i <= 58; i++) {
		cmp(93, 93, 95);
		for (int j = 0; j <= min(29, i); j++) {
			if (i - j > 29) continue;
			add(94, 32 + i - j + 1, 62 + j + 1);
			cmp(94, 3, 94);
			add(93, 93, 94);
		}
		for (int j = 1; j <= i; j++) add(93, 93, 93);
		add(2, 2, 93);
	}
#ifndef DEBUG
	printf("%d\n", (int)ans.size());
	for (auto i : ans) printf("%c %d %d %d\n", get<0>(i), get<1>(i), get<2>(i), get<3>(i));
#else
	printf("%d\n", a[2]);
#endif
	return 0;
}

此时操作次数为 $5673$ 。

然后考虑优化。

首先，竖式乘法部分，我们可以将所有 $i + j$ 相同的点加起来一起处理，这样复杂度就变成了 $O(\log ^ 2 V)$ 。
以及可以使用秦九韶算法优化（houzhiyuan 的做法），也就是将结果当成一个 $x = 2$ 的多项式，然后加速计算。

for (int i = 58; i >= 0; i--) {
    if (i != 58) add(2, 2, 2);
    for (int j = 0; j <= min(29, i); j++) {
        if (i - j > 29) continue;
        add(94, 32 + i - j + 1, 62 + j + 1);
        cmp(94, 3, 94);
        add(2, 2, 94);
    }
}

此时次数为 $3902$ 。

记录：Submission #43275171。

然后在二进制拆分 $a _ 1$ 时，我们可以新开一个内存单元而不是清空 $a _ {93}$ ，这样次数变为 $3901$ ，内存单元个数变为 $97$ 。

接下来转而优化二进制拆分部分。

我们发现可以直接把值赋给存储二进制的内存单元而不是先存到 $a _ {94}$ 这个临时变量中，这样再把值赋给 $a _ {94}$ 时就可以直接进行一次 $\times 2$ ，次数减少 $2 \times 29 = 58$ 。
另外，当 $i = 0$ 时我们只需要前两个操作（求值，赋值给存储二进制的内存单元），又可以减少 $2 \times 2 = 4$ 次操作。

for (int i = 29; i >= 0; i--) {
    add(94, 93, 3 + i);
    cmp(32 + i + 1, 94, 0);
    if (i) {
        add(94, 32 + i + 1, 32 + i + 1);
        for (int j = 1; j < i; j++) add(94, 94, 94);
        add(93, 93, 94);
    }
}

此时次数为 $3839$ 。

记录：Submission #43287946。

接下来是质的飞跃。

我们发现之前的做法中竖式乘法的 $\log ^ 2$ 部分有高达 $3$ 的常数，尝试去优化它。
发现 $x \mathbin{\mathrm{and}} y = (x \mathbin{\mathrm{xor}} 1) < y$ ，所以我们考虑将 $a _ 0$ 取反，这样就减少了 $1$ 倍常数。

我们发现原本确定 $a _ 0$ 某一位的值时，是求 $[a _ {94} < a _ 0 + 1]$ ，那么取反之后就变成 $[a _ {94} \ge a _ 0 + 1]$ ，即 $[a _ 0 < a _ {94}]$ ，那么我们只要不在最开始让 $a _ 0 \gets a _ 0 + 1$ 就好了。

但是我们更新 $a _ {93}$ 时还需要 $a _ 0$ 这一位真实的值，所以无法使用上面说的在赋值时直接 $\times 2$ 的优化。

for (int i = 29; i >= 0; i--) {
    add(94, 93, 3 + i);
    cmp(32 + i + 1, 0, 94);
    if (i) {
        cmp(94, 32 + i + 1, 3);
        for (int j = 1; j <= i; j++) add(94, 94, 94);
        add(93, 93, 94);
    }
}
// ...
for (int i = 58; i >= 0; i--) {
    if (i != 58) add(2, 2, 2);
    for (int j = 0; j <= min(29, i); j++) {
        if (i - j > 29) continue;
        cmp(94, 32 + i - j + 1, 62 + j + 1);
        add(2, 2, 94);
    }
}

次数为 $2967$ 。

记录：Submission #43288524。

接下来时一个常数优化。

我们发现在二进制拆分时的第一步 $a _ {93}$ 是空的，所以没必要去 $a _ {94}$ 那边转一下，这样就减少了 $2 \times 1$ 次。

此时次数为 $2965$ 。

记录：Submission #43288916。

看起来没有优化空间了？

并不是，在询问 yyandy 后，我学习到了一种更加优秀的求取反后二进制的方法，可以把之前抛弃的直接 $\times 2$ 优化搞回来。

那就是，我们记录 $2 ^ {30}$ ，然后用 $a _ 0 + 2 ^ i$ 与其比大小。若 $a _ 0 + 2 ^ i \ge 2 ^ {30}$ ，则 $a _ 0$ 这一位是 $1$ ，否则是 $0$ 。于是我们只要求 $[2 ^ {30} < a _ 0 + 2 ^ i]$ 就能获得 $a _ 0$ 这一位取反后的结果。在求完值后将 $a _ 0$ 这一位设为 $1$ 即可。
缺点是无法使用上面的第一步优化。

add(93, 3 + 29, 3 + 29);
for (int i = 29; i >= 0; i--) {
    add(94, 0, 3 + i), cmp(32 + i + 1, 94, 93);
    if (i) {
        add(94, 32 + i + 1, 32 + i + 1);
        for (int j = 1; j < i; j++) add(94, 94, 94);
        add(0, 0, 94);
    }
}

次数： $2938$ 。

记录：Submission #43292834。

yyandy 大概是没有使用第一步优化，所以次数比我多了 $1$ ，让我侥幸获得最优解。

最后啊，我们发现已经不需要清零操作了，所以 $a _ {95}$ 已经没用了，那么将所有 $a _ {96}$ 替换为 $a _ {95}$ 就可以让内存单元数量变回 $96$ 。

完整代码：

// Think twice, code once.
#include <tuple>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
// #define DEBUG
using namespace std;

long long a[1005];
vector<tuple<char, int, int, int>> ans;

void cmp(int i, int j, int k) {ans.emplace_back('<', j, k, i); a[i] = a[j] < a[k]; return ;}
void add(int i, int j, int k) {ans.emplace_back('+', j, k, i); a[i] = a[j] + a[k]; return ;}

int main() {
#ifdef DEBUG
	scanf("%lld%lld", &a[0], &a[1]);
#endif
	add(3, 0, 1);
	cmp(3, 4, 3);
	add(1, 1, 3);
	for (int i = 1; i <= 29; i++) add(3 + i, 3 + i - 1, 3 + i - 1);
	// for each i in 3 ~ 32: 2 ^ {i - 3}
	// 93: temp value
	// 95: the other temp value
	// 94: temp digit
	add(93, 3 + 29, 3 + 29);
	for (int i = 29; i >= 0; i--) {
		add(94, 0, 3 + i), cmp(32 + i + 1, 94, 93);
		if (i) {
			add(94, 32 + i + 1, 32 + i + 1);
			for (int j = 1; j < i; j++) add(94, 94, 94);
			add(0, 0, 94);
		}
	}
	// for each i in 33 ~ 62: x's (i - 33)th digit in binary.
	for (int i = 29; i >= 0; i--) {
		if (i != 29) add(94, 95, 3 + i), cmp(62 + i + 1, 94, 1);
		else add(95, 95, 3 + i), cmp(62 + i + 1, 95, 1);
		if (i) {
			if (i != 29) {
				add(94, 62 + i + 1, 62 + i + 1);
				for (int j = 1; j < i; j++) add(94, 94, 94);
				add(95, 95, 94);
			} else {
				add(95, 62 + i + 1, 62 + i + 1);
				for (int j = 1; j < i; j++) add(95, 95, 95);
			}
		}
	}
	// for each i in 63 ~ 92: y's (i - 63)th digit in binary.
	for (int i = 58; i >= 0; i--) {
		if (i != 58) add(2, 2, 2);
		for (int j = 0; j <= min(29, i); j++) {
			if (i - j > 29) continue;
			cmp(94, 32 + i - j + 1, 62 + j + 1);
			add(2, 2, 94);
		}
	}
#ifndef DEBUG
	printf("%d\n", (int)ans.size());
	for (auto i : ans) printf("%c %d %d %d\n", get<0>(i), get<1>(i), get<2>(i), get<3>(i));
#else
	printf("%lld\n", a[2]);
#endif
	return 0;
}

次数： $2938$ 。内存单元个数： $96$ 。

记录：Submission #43294401。

洛谷 P9348 小园香径独徘徊 [!!]

$\verb|tags: 字符串|$

很不错的一道题。

首先 $O(n ^ 2)$ 是好想的。
考虑没有 3 操作的情况，显然是贪心，能加前面就加前面，否则加后面。
然后考虑加入操作 3，显然其操作的是一段后缀。不妨考虑枚举前两种操作与第三种操作的段点，然后考虑操作 3 的影响。
不难发现这段后缀是与第一种操作得到的字符串进行归并排序式的插入，因为操作 1 得到的字符串是单调不降的，所以可以贪心解决：每次放入较小的字符，如果相同就放操作 3 得到的字符串中的字符。

然后考虑优化。

首先，可以确定断点一定在最后一个最小的字符之后，证明略。

另外可以观察发现一个结论：操作 3 的后缀一定满足其存在一个 border 是字典序最小的后缀或其本身是字典序最小的后缀。
更进一步，操作 3 的后缀 $s$ 一定满足对于其他任意后缀 $t$ ， $\forall i \le \min\left\{|s|, |t|\right\}, s _ i = t _ i$ 。

观察可以发现满足条件的后缀按长度从大到小排列后后一个一定是前一个的 border。

于是我们求出最长的满足条件的串，就可以知道所有满足条件的串。
一种方法是，跑一遍 KMP 求出 $next$ 之后，在建出来的树上，从字典序最小的后缀开始往下搜，每次选择字典序最小的儿子直到叶子。两个后缀的比较需要 SA。
不过有另一种更好的方法，就是在最后添加一个字典序极大的字符，然后求最小表示法。

但是这样我们得到的后缀还是 $O(n)$ 级别的，考虑继续优化枚举个数。

结论：对于求出来的串的所有 border 构成的 $O(\log)$ 个等差数列中，答案只可能是每个等差数列中最长的一个或最短的两个。

证明：

对于每个等差数列：

其中每个 border 对应的 period，分别是最小的 period（最长的 border 对应的 period）的 $1$ 倍、 $2$ 倍、 $3$ 倍……

也就是说，每个 border 都是最小的 period 的一个前缀，前面接若干个该 period。

其中，最短的 border 对应该 period 的一个前缀。次短的 border 对应最短的 border 前接 $1$ 个该 period……

我们考虑除了前 $2$ 以外相邻两个 border。

我们把在前面接一个 period 视为在后面补完上一个 period 并添加一个前缀。那么可以发现后面接的字符串一定是在之前基础上连在一起的。并且每次添加的字符串都是相同的，故要么不添加，要么添加到极限，对应次小和最大的 border。

所以只可能取最小、次小和最大的 border。

这样可行的字符串就只有 $O(\log)$ 个了。每次判断是 $O(n)$ 的，总时间复杂度为 $O(n \log n)$ 。

CF1172F Nauuo and Bug [!]

考虑 $-p$ 的次数。

不妨设 $c _ i$ 表示当前区间若 $- ip$ 需要的最小的初值。
容易发现 $c _ i$ 是单调的。所以若我们能奖询问划分成若干个区间并求出每个区间的 $c$ ，则可以通过二分快速得到答案。

于是考虑线段树。
考虑如何合并两个区间。
设 $sum _ l$ 为左儿子区间的和， $sum _ r$ 为右儿子区间的和， $c _ l, c _ r$ 同理。则：

c _ z = \min(\max({c _ l} _ x, {c _ r} _ y - sum _ l + xp))

前提条件是 $x + y = z, {c _ l} _ {x + 1} - 1 + sum _ l - xp \ge {c _ r} _ y$ 。

直接维护是 $O(n \log ^ 2 n)$ 的，考虑优化。
尝试能否双指针。发现可行当且仅当 ${c _ l} _ {x + 1} - 1 + sum _ l - xp$ 具有单调性，即 $c _ {i + 1} - c _ i \ge p$ 。显然是对的。

然后就做完了。

JOI Open 2022 放学路 [!!++]

$\verb|tags: 图论|$

先任意求出一条 $1$ 到 $n$ 的最短路。

我们发现这种东西一定是不合法的：

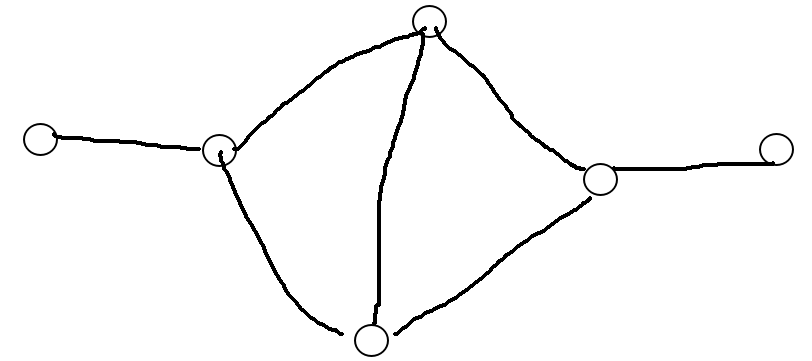
如果有一个点向这条路径连了三条边就寄了：

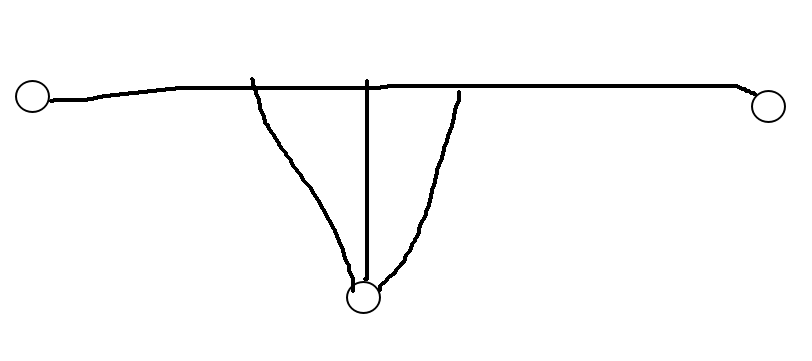
途中两条路径必有一条不合法。

如果有一个点向这条路径只连了零或一条边，那么可以直接不管。

然后只剩连两条边的情况。

发现这种也不合法：

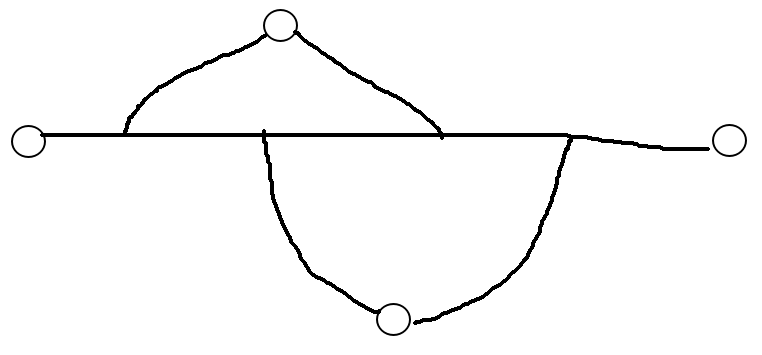
所以合法的图一定是若干个这种东西（zyk 称之为西瓜）的嵌套：

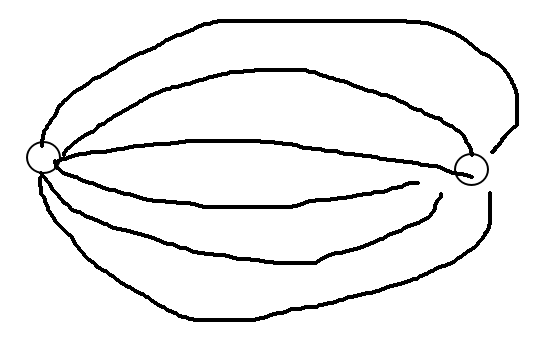
于是就有了这么一个做法：

对于两点之间的重边，若边权相同则缩成一条边，否则缩完后将边权记为 $-1$ 。对于一个 $2$ 度点，新建一条连接其连接的两个点的边，边权为两条边边权之和。最后如果 $1$ 到 $n$ 只连了一条边权不为 $-1$ 的点则输出 0，否则输出 1。

具体实现时，我们可以连一条 $1$ 到 $n$ 边权为最短路的边，然后只考虑这两个点所在的点双。

NOI2016 循环之美

$\verb|tags: 数论|$

若 $\dfrac{x}{y}$ 在 $k$ 进制下为纯循环小数，且循环节长度为 $l$ ，则：

\dfrac{x}{y} - \left\lfloor\dfrac{x}{y}\right\rfloor = \dfrac{xk ^ l}{y} - \left\lfloor\dfrac{xk ^ l}{y}\right\rfloor \iff x - \left\lfloor\dfrac{x}{y}\right\rfloor \cdot y = xk ^ l - \left\lfloor\dfrac{xk ^ l}{y}\right\rfloor \cdot y \iff \\ x \equiv xk ^ l \pmod{y} \iff k ^ l \equiv 1 \pmod{y} \iff (k, y) = 1

于是问题转化为求：

\sum\limits _ {i = 1} ^ n \sum\limits _ {j = 1} ^ m [(i, j) = 1] [(j, k) = 1]

推导一下：

\begin{aligned} & \sum\limits _ {i = 1} ^ n \sum\limits _ {j = 1} ^ m [(i, j) = 1] [(j, k) = 1] \\ = & \sum\limits _ {i = 1} ^ n \sum\limits _ {j = 1} ^ m \sum\limits _ {d \mid i, d \mid j} \mu(d) [(j, k) = 1] \\ = & \sum\limits _ {d = 1} ^ {\min\{n, m\}} \mu(d) \sum\limits _ {i = 1} ^ {\left\lfloor\frac{n}{d}\right\rfloor} \sum\limits _ {j = 1} ^ {\left\lfloor\frac{m}{d}\right\rfloor} [(j, k) = 1] \\ = & \sum\limits _ {d = 1} ^ {\min\{n, m\}} \mu(d) \left\lfloor\dfrac{n}{d}\right\rfloor [(d, k) = 1] \sum\limits _ {j = 1} ^ {\left\lfloor\frac{m}{d}\right\rfloor} [(j, k) = 1] \\ \end{aligned}

令 $g(n) = \sum _ {i = 1} ^ n [(i, k) = 1]$ 。

容易发现 $g(n) = \left\lfloor\dfrac{n}{k}\right\rfloor \varphi(k) + g(n \bmod k)$ ，这个可以 $O(k)$ 预处理得到。

于是原式变为：

\sum\limits _ {d = 1} ^ {\min\{n, m\}} (\mu(d)[(d, k) = 1]) \left(\left\lfloor\dfrac{n}{d}\right\rfloor g\left(\dfrac{m}{d}\right)\right)

考虑整除分块，问题转化为快速求前两项前缀和。

设 $S(n) = \sum _ {i = 1} ^ n \mu(i)[(i, k) = 1]$ 。考虑杜教筛：

\begin{aligned} S(n) & = \sum\limits _ {i = 1} ^ n \mu(i) [(i, k) = 1] \\ & = \sum\limits _ {i = 1} ^ n[(i, k) = 1] S\left(\left\lfloor\dfrac{n}{i}\right\rfloor\right) - \sum\limits _ {i = 2} ^ n[(i, k) = 1] S\left(\left\lfloor\dfrac{n}{i}\right\rfloor\right) \end{aligned}

$f(n) = [(n, k) = 1]$ 的前缀和就是上面的 $g(n)$ ，所以只要能快速计算左边的 $\sum$ 就行了。

\begin{aligned} & \sum\limits _ {i = 1} ^ n[(i, k) = 1] S\left(\left\lfloor\dfrac{n}{i}\right\rfloor\right) \\ = & \sum\limits _ {i = 1} ^ n[(i, k) = 1] \sum\limits _ {j = 1} ^ {\lfloor\frac{n}{i}\rfloor} \mu(j) [(j, k) = 1] \\ = & \sum\limits _ {i' = 1} ^ n [(i', k) = 1] \sum\limits _ {j \mid i'} \mu(j) \\ = & \sum\limits _ {i' = 1} ^ n [(i', k) = 1] [i' = 1] \\ = & 1 \end{aligned}

USACO20JAN Falling Portals P

$\verb|tags: 计算几何, 图论, 树, 倍增|$

考虑两个点 $i, j$ 相遇的时间。
设其为 $k$ ，则 $a _ i - ik = a _ j - jk \iff a _ i - a _ j = k(i - j) \iff k = \dfrac{a _ i - a _ j}{i - j}$ 。
也就是说相遇时间就是两点之间的斜率。（当然必须是正的）

稍微观察一下就会发现如果要从 $i$ 到 $Q _ i$ 至多经过一个中转点。

经过中转点的要求是： $i$ 到中转点的斜率小于中转点到 $Q _ i$ 的斜率。此时答案为中转点到 $Q _ i$ 的斜率。
只有 $4$ 种情况（蓝色是起点，红色是终点，绿色是中转点）：

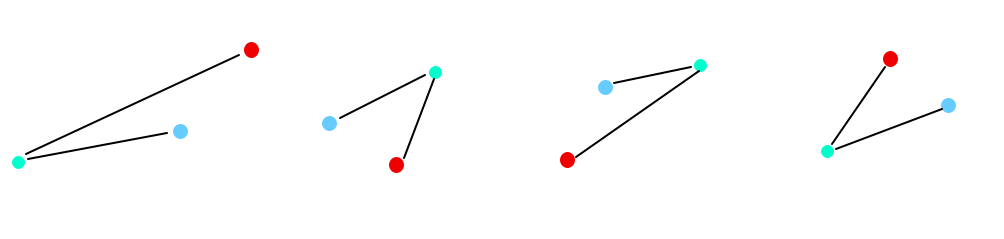
1 和 3，2 和 4 本质相同，我们只要处理其中两种，然后将图以原点中心对称再做一遍即可。

我们考虑处理 1 和 4。

对于 1：容易发现中转点是在以 $(0, 0)$ 为左下角， $(i, a _ i)$ 为右上角的矩形中的点。
对于 4：容易发现中转点是在以 $(0, 0)$ 为左下角， $(i, a _ {q _ i})$ 为右上角的矩形中的点。

也就是我们要实现每次询问一个左下角矩形中的点到某个点（在矩形右上方）的斜率最小值。

考虑没有上边界限制怎么做：单调栈维护上凸壳的前半部分（斜率为正的部分），然后二分答案。

有上凸壳限制后，我们考虑维护多个上凸壳，然后每次再对应的上凸壳上二分答案。
对于一个点，如果其可以同时属于多个上凸壳，我们让它属于最上面的那个，这样这些上凸壳就构成了一个森林。
发现询问对应的上凸壳就是矩形内最上方的点所在的上凸壳。

考虑维护这些上凸壳。如果一个点可以同时属于多个上凸壳，我们选择最上方的上凸壳即可。
此时我们惊奇地发现这和询问是等价的。

于是我们一边建树一边处理询问即可。

唯一剩下的问题就是树上二分，这个可以使用倍增解决。

// Think twice, code once.
#include <set>
#include <cmath>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

int n, a[200005], q[200005];
vector<int> b[200005];
struct Frac {
	int p, q;

	Frac() = default;
	Frac(int _p, int _q): p(_p), q(_q) {int g = __gcd(p, q); p /= g, q /= g;}
	bool operator<(const Frac &x) const {return (long long)p * x.q < (long long)x.p * q;}
	bool operator==(const Frac &x) const {return p == x.p && q == x.q;}
} ans[200005];
struct Vect {
	int x, y;

	Vect() = default;
	Vect(int _x, int _y): x(_x), y(_y) {}
	bool operator==(const Vect &a) const {return x == a.x && y == a.y;}
};
int fa[200005][20];
set<pair<int, int>> s;

int binarySearch(int h, Vect now) {
	int st = prev(s.lower_bound({h, 0}))->second;
	for (int i = 17; i >= 0; i--) {
		int to = fa[st][i];
		if (fa[to][0] == 0) continue;
		if (Frac(now.y - a[fa[to][0]], now.x - fa[to][0]) < Frac(now.y - a[to], now.x - to)) st = to;
	}
	if (fa[st][0] && Frac(now.y - a[fa[st][0]], now.x - fa[st][0]) < Frac(now.y - a[st], now.x - st))
		st = fa[st][0];
	// if (now == Vect(2, 11)) printf("%d\n", st);
	return st;
}
void solve(int op) {
	for (int i = 1; i <= n; i++) {
		if (i < q[i] && a[i] < a[q[i]] && !s.empty() && s.begin()->first < a[i]) {
			// if (i == 2) puts("?");
			int p = binarySearch(a[i], Vect(q[i], a[q[i]]));
			ans[!op ? i : n - i + 1] = min(ans[!op ? i : n - i + 1], Frac(a[q[i]] - a[p], q[i] - p));
		}

		for (int j : b[i])
			if(!s.empty() && s.begin()->first < a[j]) {
				// if (j == 2) puts("?");
				int p = binarySearch(a[j], Vect(i, a[i]));
				ans[!op ? j : n - j + 1] = min(ans[!op ? j : n - j + 1], Frac(a[i] - a[p], i - p));
			}

		if (s.empty() || s.begin()->first > a[i]) {s.emplace(a[i], i); continue;}
		fa[i][0] = binarySearch(a[i], Vect(i, a[i]));
		for (int j = 1; j <= 17; j++) fa[i][j] = fa[fa[i][j - 1]][j - 1];
		s.emplace(a[i], i);
	}
	return ;
}

int main() {
	// freopen("world.in", "r", stdin);
	// freopen("world.out", "w", stdout);

	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &q[i]), ans[i] = Frac(1e9, 1);
		if (i < q[i] && a[i] < a[q[i]]) ans[i] = Frac(a[q[i]] - a[i], q[i] - i);
		if (q[i] < i && a[q[i]] < a[i]) ans[i] = Frac(a[i] - a[q[i]], i - q[i]);
	}

	for (int i = 1; i <= n; i++)
		if (q[i] < i && a[i] < a[q[i]])
			b[q[i]].push_back(i);
	solve(0);

	reverse(a + 1, a + n + 1);
	reverse(q + 1, q + n + 1);
	for (int i = 1; i <= n; i++) a[i] = -a[i], q[i] = n - q[i] + 1, vector<int>().swap(b[i]);
	memset(fa, 0, sizeof(fa));
	set<pair<int, int>>().swap(s);

	for (int i = 1; i <= n; i++)
		if (q[i] < i && a[i] < a[q[i]])
			b[q[i]].push_back(i);
	solve(1);

	for (int i = 1; i <= n; i++)
		if (ans[i].p == 1e9) puts("-1");
		else printf("%d/%d\n", ans[i].p, ans[i].q);
	return 0;
}

分类

文章目录