2024 年 8 月做题记录

前言

会在题目名称后给每道题目一个标记，标 ! 的是我认为非常好的 CNOI-Style 的题，标 * 的是构造题、结论题等比较 Ad-hoc 的题，标 + 的是思维含量比较高题。根据牛牛程度会增减数量。

QOJ6345 Random Interactive Convex Hull Bot [**+]

考虑增量构造，每次加入一个点 $i$ 时，任意选凸包上的一个点 $s$，找到距他凸包大小一半的点 $t$，询问 $(s, t, i)$ 即可得到 $i$ 在直线 $st$ 的哪一边，然后将 $s$ 和这边的凸包上的点连线将这个半平面划分成若干部分，此时可以二分出 $i$ 在哪一部分。

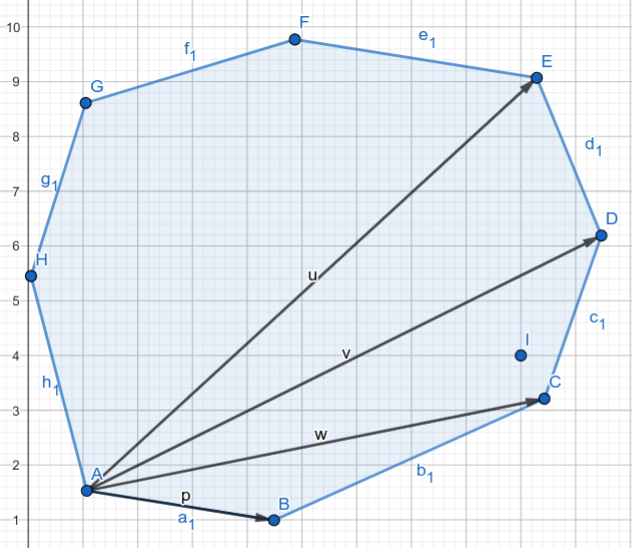
之后直接把 $i$ 两侧要删掉的点弹弹掉就好了。

CFgym104065B Call Me Call Me（2022 CCPC 绵阳）

考虑所有区间都有交怎么做。

那按交把整个序列划分成两部分，对于每一部分把每个区间按端点排序（右半部分按右端点从小到大排序，左半部分按左端点从大到小排序），然后对于每一半的每个元素给他一个 $k / 2$ 的权值，每次更新就是把所有包含它的区间的权值都 $-1$，然后取出所有权值变成 $0$ 的区间 check 一下是否满足条件，不满足就把两边都设成当前还需要的个数 $/ 2$。

这个东西应该叫折半报警器？然后这样每个区间被 check 的次数就是 $O(\log n)$ 的。

然后考虑更一般的情况。

设初始区间为 $[1, n]$，在区间中间设一个点，然后把区间划分成两部分递归下去。然后对于询问的每个区间就把他挂在第一个被他包含的点上。这样复杂度就是 $O(n\log^2 n)$。

洛谷 P7111 青春有悔

先变成求总分 $<y$ 的方案数。

设：

$$F(x) = \frac{1}{1 - x} \prod\limits_{i = 1}^n \frac{1 - x^{a_i + 1}}{1 - x}$$

在不乘前面的 $\frac{1}{1 - x}$ 时其 $i$ 次项系数就是总分为 $i$ 的方案数，乘上之后就是前缀和，即总分 $\le i$ 的方案数。

$$F(x) = \frac{1}{1 - x} \prod\limits_{i = 1}^n \frac{1 - x^{a_i + 1}}{1 - x} = \left(\frac{1}{1 - x}\right)^{n + 1} \prod\limits_{i = 1}^n (1 - x^{a_i + 1})$$

对于前半部分可以归纳证明得到：

$$\left(\frac{1}{1 - x}\right)^{n + 1} = \sum\limits_{i = 0}^\infty \binom{n + i}{i} x^i$$

对于后半部分，先 ln 一下：

$$\ln\left(\prod\limits_{i = 1}^n (1 - x^{a_i + 1})\right) = \sum\limits_{i = 1}^n \ln(1 - x^{a_i + 1}) = \sum\limits_{i = 1}^n \sum\limits_{j = 1}^\infty -\frac{x^{(a_i + 1)j}}{j}$$

对每个 $k$ 求出 $a_i + 1 = k$ 的个数可以调和级数求出每一项系数，然后 exp 一下就好了。

接着考虑一个询问 $p, b, y + 1$，那么答案就是：

$$[x^{y}]\frac{1 - x^{b + 1}}{1 - x^{a_p + 1}}F(x) = [x^{y}]\frac{1}{1 - x^{a_p + 1}}F(x) - [x^{y - b - 1}]\frac{1}{1 - x^{a_p + 1}}F(x)$$

因此问题就转化成求 $[x^y]\frac{1}{1 - x^a}F(x)$。

根号分治一下，对于 $a > B$，暴力卷积，复杂度为 $O(n\frac{n}{B})$，对于 $a \le B$，预处理出所有系数，复杂度为 $O(nB)$。取 $B = \sqrt{n}$，时间复杂度为 $O(n\sqrt{n})$。

tips：这里认为 $n, q$ 和值域同阶。

AGC062B Split and Insert [!++]

考虑把操作倒过来，就是选择一个子序列提出来放到最后，然后要从目标排列变成有序的排列。

设 $f_{i, l, r}$ 表示第 $i$ 次操作前值域 $[l, r]$ 已经排好序的最小代价，则：

$$f_{i, l, r} = \min\{f_{i + 1, l, r} \cup \{f_{i + 1, l, k} + f_{i + 1, k + 1, r} + c_i (r - k) \mid l \le k < r\}\}$$

初始状态就是 $f_{m + 1, l, r} = 0$，要求目标状态值域 $[l, r]$ 的数是排好序的。答案就是 $f_{1, 1, n}$。

CF1874E Jellyfish and Hack [!]

设 $f_{i, j}$ 表示长度为 $i$ 权值为 $j$ 的排列的方案数，有如下转移：

$$f_{i, j} = \sum\limits_{k = 1}^i \binom{i - 1}{k - 1} \sum\limits_{l = 0}^{j - i} f_{k - 1, l} f_{i - k, j - i - l}$$

暴力转移是 $O(n^6)$ 的。

考虑设 $F_i(x) = \sum_{j = 0}^{i(i + 1) / 2} f_{i, j}x^j$，显然是最高 $n(n + 1) / 2$ 次多项式，带 $n(n + 1) / 2 + 1$ 个值进去插一下就好了，每次转移是 $O(n^4)$ 的，插值后还原多项式也是 $O(n^4)$ 的。

CF1758F Decent Division [!!]

考虑对于为 $1$ 的每个位置 $i$，设 $to(i)$ 表示最小的区间使得 $[i, to(i)]$ 是一段合法区间。即：令 $1$ 为 $1$，$0$ 为 $-1$，设 $s_i$ 为前缀和，则 $to(i)$ 是最小的满足 $s_{to(i)} = s_{i - 1}$ 的位置。

每次操作位置 $i$ 使得 $0 \to 1$ 时，若 $i$ 不被区间包含，则令 $p = i$，否则令 $p = l$ 为包含它的区间的左端点，然后加入 $[p, to(p)]$，再删除与之相交的区间。这样调整完就合法了，因为所有 $[i, to(i)]$ 的区间要么包含要么相离。

每次操作 $1 \to 0$ 时，找到区间左端点 $l$，删掉区间，然后不断找到 $l$ 后第一个 $1$ 的位置 $p$，加入 $[p, to(p)]$，然后 $l \gets to(p) + 1$，直到 $p > r$。

正确性显然，但是时间有点问题，区间可能被拆成很多个，一个简单的 hack 是：操作 $1, 3, 5, 7, \ldots$，然后一直操作 $2$。

解决办法是令 $to(i)$ 为满足 $s_{to(i)} = s_{i - 1}$ 且 $\forall j \in [i, to(i)), s_j \ge s_{i - 1}$ 的最大位置，这样每次拆区间后都会在区间下一位留下一个 $0$。新选择的区间的总和相较于原区间至多 $-2$，因此最多留下 $2$ 个 $0$，因此至多被拆成 $3$ 个区间。

CF1874D Jellyfish and Miku [!+]

设 $f_i$ 表示从 $i$ 走到终点的期望步数。

$$\begin{cases} f_0 = 1 + f_1 \\ f_i = 1 + \frac{a_i}{a_i + a_{i + 1}} f_{i - 1} + \frac{a_{i + 1}}{a_i + a_{i + 1}} f_{i + 1} & 1 \le i < n \\ f_n = 0 \end{cases}$$

第二个式子化一下：

$$a_{i + 1} (f_i - f_{i + 1}) = a_i (f_{i - 1} - f_i) + a_i + a_{i + 1}$$

设 $g_i = f_{i - 1} - f_i$，则：

$$\begin{cases} g_1 = 1 \\ a_i g_i = a_{i - 1} g_{i - 1} + a_{i - 1} + a_i \end{cases}$$

可以归纳证明：

$$g_i = 2\times \frac{\sum\limits_{j = 1}^{i - 1} a_j}{a_i} + 1$$

答案即为：

$$\begin{aligned} f_0 &= \sum\limits_{i = 1}^n (f_{i - 1} - f_i) \\ &= \sum\limits_{i = 1}^n g_i \\ &= \sum\limits_{i = 1}^n \left(2\times \frac{\sum\limits_{j = 1}^{i - 1} a_j}{a_i} + 1\right) \\ &= n + 2\sum\limits_{i = 1}^n \frac{1}{a_i} \sum\limits_{j = 1}^{i - 1} a_j \end{aligned}$$

只要最小化后面那个东西即可。

设 $dp_{i, j}$ 表示前 $i$ 个，$a$ 的和是 $j$ 时的答案，有如下转移：

$$dp_{i, j + k} \gets dp_{i, j} + \frac{j}{k}$$

直接来是 $O(nm^2)$ 的，但是再仔细分析可以发现 $a$ 一定是单调不降的，因此转移时需要保证 $j + k (n - i + 1) \le m$，这样复杂度就变成了：

$$O\left(\sum\limits_{i = 1}^n \sum\limits_{j = 0}^m \frac{m - j}{i}\right) = O\left(\sum\limits_{i = 1}^n \frac{m(m + 1)}{2i}\right) = O\left(m^2\log m\right)$$

CF512E Fox And Polygon [*]

操作可逆，所以把两个凸包都变成所有弦都与 $1$ 相连。具体就是顺时针枚举每个点，然后对未符合要求的操作对角线。

CF1707E Replace [!!++]

咕了。