在本文中:
字符串索引默认从 1 1 1
用 s [ l , r ] s_{[l, r]} s [ l , r ] s l s l + 1 s l + 2 … s r s_l s_{l + 1} s_{l + 2} \ldots s_r s l s l + 1 s l + 2 … s r [ l , r ] = ∅ [l, r] = \varnothing [ l , r ] = ∅
用 p r e ( s , i ) \mathrm{pre}(s, i) p r e ( s , i ) s [ 1 , i ] s_{[1, i]} s [ 1 , i ] s u f ( s , i ) \mathrm{suf}(s, i) s u f ( s , i ) s [ i , ∣ s ∣ ] s_{[i, |s|]} s [ i , ∣ s ∣ ]
对于一个字符串 s s s i < ∣ s ∣ i<|s| i < ∣ s ∣ p r e ( s , i ) = s u f ( s , ∣ s ∣ − i + 1 ) \mathrm{pre}(s, i) = \mathrm{suf}(s, |s| - i + 1) p r e ( s , i ) = s u f ( s , ∣ s ∣ − i + 1 ) p r e ( s , i ) \mathrm{pre}(s, i) p r e ( s , i ) s s s B ( s ) \mathcal{B}(s) B ( s ) s s s s s s k < ∣ s ∣ k < |s| k < ∣ s ∣ ∀ i ∈ ( k , ∣ s ∣ ] , s i = s i − k \forall i \in (k, |s|], s_i = s_{i - k} ∀ i ∈ ( k , ∣ s ∣ ] , s i = s i − k k k k s s s k ∣ ∣ s ∣ k \mid |s| k ∣ ∣ s ∣ k k k s s s P ( s ) \mathcal{P}(s) P ( s ) s s s
例如:对于字符串 abcab \texttt{abcab} abcab ab \texttt{ab} ab 3 3 3
定理 1 :对于一个字符串 s s s t t t B ( s ) = B ( t ) ∪ { t } \mathcal{B}(s) = \mathcal{B}(t) \cup \{t\} B ( s ) = B ( t ) ∪ { t }
也就是对于一个串,除了最长的 Border 以外,其他的 Border 都是最长 Border 的 Border。s s s t t t t t t
稍微手玩一下就行,读者自证不难。
定理 2 :一个字符串的 Border 与 Period 一一对应。具体地,p r e ( s , i ) ∈ B ( s ) ⟺ ∣ s ∣ − i ∈ P ( s ) \mathrm{pre}(s, i) \in \mathcal{B}(s) \iff |s| - i \in \mathcal{P}(s) p r e ( s , i ) ∈ B ( s ) ⟺ ∣ s ∣ − i ∈ P ( s )
证明考虑分讨 i ≤ ∣ s ∣ 2 i \le \frac{|s|}{2} i ≤ 2 ∣ s ∣ i > ∣ s ∣ 2 i > \frac{|s|}{2} i > 2 ∣ s ∣
根据性质 1,我们只需要知道一个串所有前缀的最长 Border,就可以求出该串的所有 Border。
对于一个字符串 s s s ∣ s ∣ |s| ∣ s ∣ π \pi π π i \pi_i π i p r e ( s , i ) \mathrm{pre}(s,i) p r e ( s , i ) π i = 0 \pi_i = 0 π i = 0
考虑在线地求出前缀函数,也就是根据 π 1 … π i − 1 \pi_1 \ldots \pi_{i - 1} π 1 … π i − 1 π i \pi_i π i
首先容易发现,π i ≤ π i − 1 + 1 \pi_i \le \pi_{i - 1} + 1 π i ≤ π i − 1 + 1 π i > 1 \pi_i > 1 π i > 1 p r e ( s , π i − 1 ) ∈ B ( p r e ( s , i − 1 ) ) \mathrm{pre}(s, \pi_i - 1)\in\mathcal{B}(\mathrm{pre}(s, i - 1)) p r e ( s , π i − 1 ) ∈ B ( p r e ( s , i − 1 ) ) π i − 1 \pi_{i - 1} π i − 1 B ( p r e ( s , i − 1 ) ) \mathcal{B}(\mathrm{pre}(s, i - 1)) B ( p r e ( s , i − 1 ) ) j j j s j + 1 = s i s_{j + 1} = s_i s j + 1 = s i π i = j + 1 \pi_{i} = j + 1 π i = j + 1 j j j π i = [ s 1 = s i ] \pi_i = [s_1 = s_i] π i = [ s 1 = s i ]
考虑分析这个算法的时间复杂度,用一个指针维护当前最后一个位置的 π \pi π 1 1 1
参考代码:
1 2 3 4 5 for (int i = 2 , j = 0 ; i <= n; i++) { while (j && s[j + 1 ] != s[i]) j = pi[j]; if (s[j + 1 ] == s[i]) pi[i] = ++j; }
这是一个经典问题,即给定两个字符串 s , t s, t s , t t t t s s s t t t s s s
解决这个问题的朴素想法是枚举每个位置,然后将这个位置的子串与 t t t
1 2 3 4 5 6 7 8 for (int i = 1 ; i + m - 1 <= n; i++) { int flag = 1 ; for (int j = 1 ; j <= m; j++) if (s[i + j - 1 ] != t[j]) {flag = 0 ; break ;} if (flag) printf ("%d " , i); } puts ("" );
考虑优化这个暴力,去除无用的枚举。
考虑设当前起点为 i i i s s s j + 1 j + 1 j + 1 j + 1 j + 1 j + 1 l l l j − l + 1 > i , p r e ( t , l ) = s [ j − l + 1 , j ] j - l + 1 > i, \mathrm{pre}(t, l) = s_{[j - l + 1, j]} j − l + 1 > i , p r e ( t , l ) = s [ j − l + 1 , j ]
我们知道 s [ i , j ] = p r e ( t , j − i + 1 ) s_{[i, j]} = \mathrm{pre}(t, j - i + 1) s [ i , j ] = p r e ( t , j − i + 1 ) p r e ( t , l ) = t [ j − i + 1 − l + 1 , j − i + 1 ] \mathrm{pre}(t, l) = t_{[j - i + 1 - l + 1, j - i + 1]} p r e ( t , l ) = t [ j − i + 1 − l + 1 , j − i + 1 ] l l l p r e ( t , j − i + 1 ) \mathrm{pre}(t, j - i + 1) p r e ( t , j − i + 1 )
1 2 3 4 5 6 7 8 9 for (int i = 1 , j = 0 ; i <= n; i++) { while (j && t[j + 1 ] != s[i]) j = pi[j]; if (t[j + 1 ] == s[i]) if (++j == m) { j = nxt[j]; } }
容易发现 j j j 1 1 1 O ( n ) O(n) O ( n )
其实还可以从另一个角度考虑这个问题,我们讲 s s s t t t t + # + s t + \# + s t + # + s # \# # t t t s s s s s s π = ∣ t ∣ \pi = |t| π = ∣ t ∣
因为 π i ≤ ∣ t ∣ \pi_i \le |t| π i ≤ ∣ t ∣ s s s π i \pi_i π i t t t s s s π i \pi_i π i
考虑对于字符串的每个前缀建一个点,并对每个点 i i i π i \pi_i π i
对于每个前缀,其 Border 就是它在树上的所有非根祖先。
例题:CF1286E Fedya the Potter Strikes Back
给定一个字符串 S S S W W W
有 n n n S S S W W W
∑ S [ L , R ] = S [ 1 , R − L + 1 ] min i = L R W i \sum\limits_{S_{[L, R]} = S_{[1, R - L + 1]}} \min_{i = L}^R W_i
S [ L , R ] = S [ 1 , R − L + 1 ] ∑ i = L min R W i
强制在线。
1 ≤ n ≤ 6 × 1 0 5 1 \le n \le 6\times 10^5 1 ≤ n ≤ 6 × 1 0 5
TL: 4s, ML: 250MB.
只需考虑新串的所有 Border,再求前缀和即可。
容易发现新串的 Border 要么是原串的某个 Border 后面添加一个字符,要么长度为 1 1 1
考虑如何删除不合法的 Border,只需要对于每个前缀记录其第一个后继不同的祖先即可。
然后考虑更新答案,用一个 map 记录答案为某个值的区间的数量然后暴力推平,时间复杂度与颜色段均摊相同。
然后这题就做完了,时间复杂度为 O ( n log n ) O(n\log n) O ( n log n )
弱周期引理(Weak Periodicity Lemma) :
∀ p , q ∈ P ( s ) , p + q ≤ ∣ s ∣ ⟹ gcd ( p , q ) ∈ P ( s ) \forall p, q\in\mathcal{P}(s), p + q \le |s| \implies \gcd(p, q)\in\mathcal{P}(s)
∀ p , q ∈ P ( s ) , p + q ≤ ∣ s ∣ ⟹ g cd( p , q ) ∈ P ( s )
证明:
令 p < q p < q p < q d = q − p d = q-p d = q − p d ∈ P ( s ) d \in \mathcal{P}(s) d ∈ P ( s )
∀ i ∈ ( d , ∣ s ∣ − p ] , s i = s i + p = s i + p − q = s i − d \forall i \in (d, |s| - p], s_i = s_{i + p} = s_{i + p - q} = s_{i - d} ∀ i ∈ ( d , ∣ s ∣ − p ] , s i = s i + p = s i + p − q = s i − d ∀ i ∈ ( q , ∣ s ∣ ] , s i = s i − q = s i − q + p = s i − d \forall i \in (q, |s|], s_i = s_{i - q} = s_{i - q + p} = s_{i - d} ∀ i ∈ ( q , ∣ s ∣ ] , s i = s i − q = s i − q + p = s i − d
因为 p + q ≤ ∣ s ∣ p + q \le |s| p + q ≤ ∣ s ∣ q ≤ ∣ s ∣ − p q \le |s| - p q ≤ ∣ s ∣ − p ( d , ∣ s ∣ − p ] ∪ ( q , ∣ s ∣ ] = ( d , ∣ s ∣ ] (d, |s| - p] \cup (q, |s|] = (d, |s|] ( d , ∣ s ∣ − p ] ∪ ( q , ∣ s ∣ ] = ( d , ∣ s ∣ ] d ∈ P ( s ) d \in \mathcal{P}(s) d ∈ P ( s )
□ \square □
一般情况下弱周期引理就够用了,但实际上有更紧的界。
在讲周期引理之前插入一个小定理:
定理 3 :若字符串 t t t s s s a ∈ P ( s ) , b ∈ P ( t ) , b ∣ a , ∣ t ∣ ≥ a a \in \mathcal{P}(s), b \in \mathcal{P}(t), b \mid a, |t| \ge a a ∈ P ( s ) , b ∈ P ( t ) , b ∣ a , ∣ t ∣ ≥ a b b b t t t b ∈ P ( s ) b \in \mathcal{P}(s) b ∈ P ( s )
容易发现 a a a t t t b ∣ a b \mid a b ∣ a b b b s s s
周期引理(Periodicity Lemma) :
∀ p , q ∈ P ( s ) , p + q − gcd ( p , q ) ≤ ∣ s ∣ ⟹ gcd ( p , q ) ∈ P ( s ) \forall p, q\in\mathcal{P}(s), p + q - \gcd(p, q) \le |s| \implies \gcd(p, q)\in\mathcal{P}(s)
∀ p , q ∈ P ( s ) , p + q − g cd( p , q ) ≤ ∣ s ∣ ⟹ g cd( p , q ) ∈ P ( s )
证明:
令 p < q p < q p < q d = q − p d = q - p d = q − p
由于 ∀ i ∈ ( d , ∣ s ∣ − p ] , s i = s i + p = s i + p − q = s i − d \forall i \in (d, |s| - p], s_i = s_{i + p} = s_{i + p - q} = s_{i - d} ∀ i ∈ ( d , ∣ s ∣ − p ] , s i = s i + p = s i + p − q = s i − d d ∈ P ( p r e ( s , ∣ s ∣ − p ) ) d \in \mathcal{P}(\mathrm{pre}(s, |s| - p)) d ∈ P ( p r e ( s , ∣ s ∣ − p ) )
考虑归纳,假设已经证明周期引理对于 p r e ( s , ∣ s ∣ − p ) \mathrm{pre}(s, |s| - p) p r e ( s , ∣ s ∣ − p ) p + q − gcd ( p , q ) ≤ ∣ s ∣ p + q - \gcd(p, q) \le |s| p + q − g cd( p , q ) ≤ ∣ s ∣ p p p p + ( q − p ) − gcd ( p , q − p ) ≤ ∣ s ∣ − p p + (q - p) - \gcd(p, q - p) \le |s| - p p + ( q − p ) − g cd( p , q − p ) ≤ ∣ s ∣ − p gcd ( p , q ) ∈ P ( p r e ( s , ∣ s ∣ − p ) ) \gcd(p, q) \in \mathcal{P}(\mathrm{pre}(s, |s| - p)) g cd( p , q ) ∈ P ( p r e ( s , ∣ s ∣ − p ) )
因为 2 p = p + q − ( q − p ) ≤ p + q − gcd ( p , q ) ≤ ∣ s ∣ 2p = p + q - (q - p) \le p + q - \gcd(p, q) \le |s| 2 p = p + q − ( q − p ) ≤ p + q − g cd( p , q ) ≤ ∣ s ∣ p ≤ ∣ s ∣ − p p \le |s| - p p ≤ ∣ s ∣ − p gcd ( p , q ) ∈ P ( p r e ( s , p ) ) \gcd(p, q) \in \mathcal{P}(\mathrm{pre}(s, p)) g cd( p , q ) ∈ P ( p r e ( s , p ) )
由于 gcd ( p , q ) ∣ p \gcd(p, q) | p g cd( p , q ) ∣ p gcd ( p , q ) \gcd(p, q) g cd( p , q ) s [ 1 , p ] s_{[1, p]} s [ 1 , p ] gcd ( p , q ) ∈ P ( s ) \gcd(p, q) \in \mathcal{P}(s) g cd( p , q ) ∈ P ( s )
□ \square □
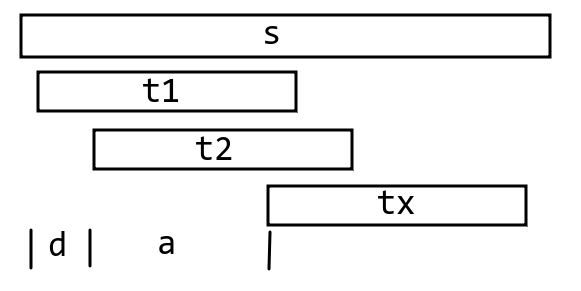
定理 4 :对于文本串 s s s t t t ∣ t ∣ ≥ ∣ s ∣ 2 |t| \ge \frac{|s|}{2} ∣ t ∣ ≥ 2 ∣ s ∣ t t t s s s 3 3 3 t t t
证明:
考虑匹配成功的第 1 1 1 2 2 2 t 1 , t 2 , t x t_1, t_2, t_x t 1 , t 2 , t x t 1 , t 2 t_1, t_2 t 1 , t 2 d d d t 2 , t x t_2, t_x t 2 , t x a a a d , a d, a d , a t t t
因为 ∣ t ∣ ≥ ∣ s ∣ 2 |t| \ge \frac{|s|}{2} ∣ t ∣ ≥ 2 ∣ s ∣ t 1 , t x t_1, t_x t 1 , t x ∣ t ∣ |t| ∣ t ∣ d + a ≤ ∣ t ∣ d + a \le |t| d + a ≤ ∣ t ∣ gcd ( d , a ) \gcd(d, a) g cd( d , a ) t t t
设 t t t p p p p ≤ gcd ( d , a ) ≤ d p \le \gcd(d, a) \le d p ≤ g cd( d , a ) ≤ d p + gcd ( d , a ) ≤ d + gcd ( d , a ) ≤ d + a ≤ ∣ t ∣ p + \gcd(d, a) \le d + \gcd(d, a) \le d + a \le |t| p + g cd( d , a ) ≤ d + g cd( d , a ) ≤ d + a ≤ ∣ t ∣ gcd ( p , d , a ) ≤ p \gcd(p, d, a) \le p g cd( p , d , a ) ≤ p p p p p ∣ gcd ( p , d , a ) p\mid\gcd(p, d, a) p ∣ g cd( p , d , a ) p ∣ d p\mid d p ∣ d
若 p ≠ d p\ne d p = d t 1 t_1 t 1 p p p p = d p = d p = d
显然上面的分析中只要满足 t x t_x t x ≥ 3 \ge 3 ≥ 3 p p p p p p
□ \square □
然而我并没有在 OI 中见到什么题目需要用到这个定理,如果有人知道请告诉我,十分感谢!
upd on 2024/10/14: 现在有了,感谢学弟让我见到了这个题!
例题:CF1038F Wrap Around
给定一个字符串,字符集为 { 0 , 1 } \{0, 1\} { 0 , 1 } n n n t t t t t t s s s
1 ≤ ∣ s ∣ ≤ n ≤ 40 1 \le |s| \le n \le 40 1 ≤ ∣ s ∣ ≤ n ≤ 4 0 4000 4000 4 0 0 0
TL: 2s, ML: 250MB.
加强到 4000 4000 4 0 0 0
考虑 s s s t t t d p i , j dp_{i, j} d p i , j i i i s s s j j j j = ∣ s ∣ j = |s| j = ∣ s ∣
然后考虑所有 s s s s s s l e n len l e n t t t s + t + s s + t + s s + t + s s s s
做法和上面的 DP 类似,将初值设为 d p 0 , π ∣ s ∣ = 1 dp_{0, \pi_{|s|}} = 1 d p 0 , π ∣ s ∣ = 1 i i i s u m i sum_i s u m i
s u m i = ∑ j ∉ P d p i , j sum_i = \sum\limits_{j \notin \mathcal{P}} dp_{i, j}
s u m i = j ∈ / P ∑ d p i , j
然后考虑 s s s
如果只放了 1 1 1 s 2 s_2 s 2 s ∣ s ∣ s_{|s|} s ∣ s ∣ ( ∣ s ∣ − 1 ) s u m n − ∣ s ∣ (|s| - 1) sum_{n - |s|} ( ∣ s ∣ − 1 ) s u m n − ∣ s ∣
如果放了 ≥ 3 \ge 3 ≥ 3 p p p i i i ( ∣ s ∣ − ( i − 1 ) p − 1 ) s u m n − ( ∣ s ∣ − ( i − 1 ) p ) (|s| - (i - 1)p - 1) sum_{n - (|s| - (i - 1)p)} ( ∣ s ∣ − ( i − 1 ) p − 1 ) s u m n − ( ∣ s ∣ − ( i − 1 ) p ) s s s ( i − 1 ) p < ∣ s ∣ (i - 1)p < |s| ( i − 1 ) p < ∣ s ∣
如果放了 2 2 2 s s s i i i ( i − 1 ) s u m n − ( 2 ∣ s ∣ − i ) (i - 1) sum_{n - (2|s| - i)} ( i − 1 ) s u m n − ( 2 ∣ s ∣ − i )
注意需要保证 s s s ≤ n \le n ≤ n
但是这样仍是有问题的,考虑 n = 5 , s = 101 n = 5, s = \verb|101| n = 5 , s = 101 2 2 2 ≥ 2 \ge 2 ≥ 2 ≥ n \ge n ≥ n
定理 5 :一个字符串 s s s ∣ s ∣ 2 \frac{|s|}{2} 2 ∣ s ∣
证明:
设最长的 Border 的长度为 ∣ s ∣ − p |s| - p ∣ s ∣ − p ∣ s ∣ − q |s| - q ∣ s ∣ − q p , q ≤ ∣ s ∣ 2 p, q \le \frac{|s|}{2} p , q ≤ 2 ∣ s ∣
由弱周期引理可知 gcd ( p , q ) \gcd(p, q) g cd( p , q ) s s s p ≤ gcd ( p , q ) p \le \gcd(p, q) p ≤ g cd( p , q ) p ∣ q p \mid q p ∣ q
容易发现每次将最长的 Border 删去最后 p p p ∣ s ∣ 2 \frac{|s|}{2} 2 ∣ s ∣
□ \square □
定理 6 :一个字符串的所有 Border 的长度排序后可以划分成 ⌈ log 2 ∣ s ∣ ⌉ \lceil\log_2|s|\rceil ⌈ log 2 ∣ s ∣ ⌉
首先可以将定理 5 扩展一下,把 ∣ s ∣ |s| ∣ s ∣
这样每次取出长度大于 ∣ s ∣ 2 \frac{|s|}{2} 2 ∣ s ∣ s s s
□ \square □
基于定理 5 和定理 6,可以大大优化寻找 Border 和处理 Border 的复杂度。
例题:WC2016 论战捆竹竿
给定长度为 n n n s s s t t t a a a s u f ( t , ∣ t ∣ − a + 1 ) = p r e ( s , a ) \mathrm{suf}(t, |t| - a + 1) = \mathrm{pre}(s, a) s u f ( t , ∣ t ∣ − a + 1 ) = p r e ( s , a ) t ← t + s u f ( s , a + 1 ) t \gets t + \mathrm{suf}(s, a + 1) t ← t + s u f ( s , a + 1 ) ∣ t ∣ ≤ w |t| \le w ∣ t ∣ ≤ w ∣ t ∣ |t| ∣ t ∣
多组数据,T ≤ 5 , n ≤ 5 × 1 0 5 , w ≤ 1 0 18 T\le 5, n\le 5\times 10^5, w\le 10^{18} T ≤ 5 , n ≤ 5 × 1 0 5 , w ≤ 1 0 1 8
TL: 1s, ML: 120MB.
显然除了第一次外 a a a s s s ∑ a i x i \sum a_i x_i ∑ a i x i [ 0 , w − ∣ s ∣ ] [0, w - |s|] [ 0 , w − ∣ s ∣ ] a i a_i a i s s s
然后考虑同余最短路,朴素做法是 O ( min P ( s ) × ∣ P ( s ) ∣ ) = O ( ∣ s ∣ 2 ) O(\min\mathcal{P}(s) \times |\mathcal{P}(s)|) = O(|s|^2) O ( min P ( s ) × ∣ P ( s ) ∣ ) = O ( ∣ s ∣ 2 )
考虑对每个等差数列分开来处理。对于一个等差数列 x , x + d , … , x + k d x, x + d, \ldots, x + kd x , x + d , … , x + k d m o d x {}\bmod x m o d x + 0 , + d , + 2 d , … , + k d +0, +d, +2d, \ldots, +kd + 0 , + d , + 2 d , … , + k d gcd ( x , d ) \gcd(x, d) g cd( x , d )
然后剩下来的问题就是合并,也就是要求模数改变后的结果。
设在模 p r e pre p r e f f f n o w now n o w g g g g i = min f j ≡ i ( m o d n o w ) f j g_i = \min_{f_j \equiv i \pmod{now}} f_j g i = min f j ≡ i ( m o d n o w ) f j
然后由于 f i f_i f i f i + k × p r e f_i + k\times pre f i + k × p r e g g g g i g_i g i g i + k × p r e g_{i + k\times pre} g i + k × p r e
时间复杂度为 O ( T n log n ) O(Tn\log n) O ( T n log n )
定理 7 :回文串的回文前/后缀即为该串的 Border。
一般是根据这个性质可以把回文前缀转化成 Border 然后用定理 5 和定理 6优化。
定理 8 :若回文串 s s s p p p p r e ( s , p ) \mathrm{pre}(s, p) p r e ( s , p ) ∣ s ∣ m o d p |s| \bmod p ∣ s ∣ m o d p p − ∣ s ∣ m o d p p - |s| \bmod p p − ∣ s ∣ m o d p
画下图就明白了:
语言描述的严谨证明 :
用 r e v ( s ) \mathrm{rev}(s) r e v ( s ) s s s p r e ( s , ∣ s ∣ m o d p ) = r e v ( s u f ( s , ∣ s ∣ − ∣ s ∣ m o d p + 1 ) ) \mathrm{pre}(s, |s|\bmod p) = \mathrm{rev}(\mathrm{suf}(s, |s| - |s| \bmod p + 1)) p r e ( s , ∣ s ∣ m o d p ) = r e v ( s u f ( s , ∣ s ∣ − ∣ s ∣ m o d p + 1 ) ) p r e ( s , ∣ s ∣ m o d p ) = s u f ( s , ∣ s ∣ − ∣ s ∣ m o d p + 1 ) \mathrm{pre}(s, |s|\bmod p) = \mathrm{suf}(s, |s| - |s| \bmod p + 1) p r e ( s , ∣ s ∣ m o d p ) = s u f ( s , ∣ s ∣ − ∣ s ∣ m o d p + 1 ) p r e ( s , ∣ s ∣ m o d p ) \mathrm{pre}(s, |s|\bmod p) p r e ( s , ∣ s ∣ m o d p )
考虑字符串 s ( ∣ s ∣ m o d p , s − ∣ s ∣ m o d p ] s_{(|s|\bmod p, s - |s|\bmod p]} s ( ∣ s ∣ m o d p , s − ∣ s ∣ m o d p ] p p p p p p s ( ∣ s ∣ m o d p , p ] s_{(|s|\bmod p, p]} s ( ∣ s ∣ m o d p , p ] s ( ∣ s ∣ m o d p , p ] s_{(|s|\bmod p, p]} s ( ∣ s ∣ m o d p , p ]
□ \square □
定理 9 :若 t t t s s s ∣ t ∣ ≥ ∣ s ∣ 2 |t| \ge \frac{|s|}{2} ∣ t ∣ ≥ 2 ∣ s ∣ t t t s s s 2 2 2
证明考虑反证,如果超过 2 2 2
这两个定理也没有找到什么应用……
记 S s u f ( s ) \mathrm{Ssuf}(s) S s u f ( s ) s s s t ∈ S s u f ( s ) ⟺ t\in \mathrm{Ssuf}(s) \iff t ∈ S s u f ( s ) ⟺ u u u t + u t + u t + u s + u s + u s + u
定理 10 :对于任意一个字符串以及 u , v ∈ S s u f ( s ) , ∣ u ∣ < ∣ v ∣ u, v\in\mathrm{Ssuf}(s), |u| < |v| u , v ∈ S s u f ( s ) , ∣ u ∣ < ∣ v ∣ u u u v v v
显然。
定理 11 :对于任意一个字符串 s s s u , v ∈ S s u f ( s ) , ∣ u ∣ < ∣ v ∣ u, v\in\mathrm{Ssuf}(s), |u| < |v| u , v ∈ S s u f ( s ) , ∣ u ∣ < ∣ v ∣ 2 ∣ u ∣ ≤ ∣ v ∣ 2|u| \le |v| 2 ∣ u ∣ ≤ ∣ v ∣
证明:
由定理 10 可得 u u u v v v
假设 2 ∣ u ∣ > ∣ v ∣ 2|u| > |v| 2 ∣ u ∣ > ∣ v ∣ u u u p p p t = p r e ( v , p ) t = \mathrm{pre}(v, p) t = p r e ( v , p ) u , v u, v u , v u = t + w , v = t + t + w u = t + w, v = t + t + w u = t + w , v = t + t + w
若存在一个字符串 r r r u + r < v + r u + r < v + r u + r < v + r t + w + r < t + t + w + r t + w + r < t + t + w + r t + w + r < t + t + w + r w + r < t + w + r w + r < t + w + r w + r < t + w + r w + r < u + r w + r < u + r w + r < u + r r r r u + r < w + r u + r < w + r u + r < w + r u + r < v + r u + r < v + r u + r < v + r u ∉ S s u f ( s ) u \notin \mathrm{Ssuf}(s) u ∈ / S s u f ( s )
□ \square □
定理 12 :∣ S s u f ( s ) ∣ ≤ log 2 ∣ s ∣ |\mathrm{Ssuf}(s)| \le \log_2|s| ∣ S s u f ( s ) ∣ ≤ log 2 ∣ s ∣
由定理 11 可得。
例题:ZJOI2017 字符串
维护一个动态字符串 s 1.. n s_{1..n} s 1 . . n ∣ x ∣ ≤ 1 0 9 |x| \le 10^9 ∣ x ∣ ≤ 1 0 9
输入 l , r , d l, r, d l , r , d l ≤ i ≤ r l \le i \le r l ≤ i ≤ r s i s_i s i s i + d s_i + d s i + d d d d
输入 l , r l, r l , r s l . . r s_{l..r} s l . . r s p . . r s_{p..r} s p . . r l ≤ p ≤ r l \le p \le r l ≤ p ≤ r p p p
1 ≤ n ≤ 2 × 1 0 5 , 1 ≤ q ≤ 3 × 1 0 4 , ∣ s i ∣ ≤ 1 0 8 , ∣ d ∣ ≤ 1 0 3 1 \le n \le 2\times 10^5, 1 \le q \le 3\times 10^4, |s_i| \le 10^8, |d| \le 10^3 1 ≤ n ≤ 2 × 1 0 5 , 1 ≤ q ≤ 3 × 1 0 4 , ∣ s i ∣ ≤ 1 0 8 , ∣ d ∣ ≤ 1 0 3
TL: 3s, ML: 500MB.
用线段树维护,在线段树每个节点上维护这个区间的 S s u f \mathrm{Ssuf} S s u f S s u f \mathrm{Ssuf} S s u f
这样已经可以保证每个节点是 O ( log n ) O(\log n) O ( log n ) S s u f \mathrm{Ssuf} S s u f
对于查询,由于只会找到线段树上 O ( log n ) O(\log n) O ( log n ) O ( log 2 n ) O(\log^2 n) O ( log 2 n )
后缀大小比较需要二分加哈希,由于有修改操作,哈希值也许要数据结构维护。如果用线段树,则复杂度为 O ( n log 3 n + m log 4 n ) O(n\log^3 n + m\log^4 n) O ( n log 3 n + m log 4 n ) O ( n ) O(\sqrt{n}) O ( n ) O ( 1 ) O(1) O ( 1 ) O ( n log 2 n + m log 3 n + m n ) O(n\log^2 n + m\log^3 n + m\sqrt{n}) O ( n log 2 n + m log 3 n + m n )