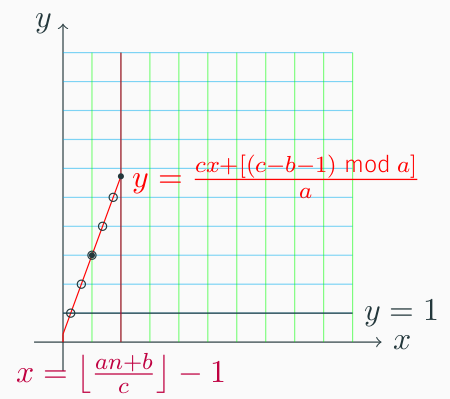问题描述
给出一个幺半群 (S,⋅) 和元素 u,r∈S,以及一条直线 y=cax+b。
画出平面中所有坐标为正整数的横线和竖线,维护一个 f,初值为单位元 e。
从原点出发,先向 y 轴正方向走直到到达直线与 y 的交点,然后沿直线走一直走到与 x=n 的交点为止。
每当经过一条横线时,执行 f←fu,经过一条竖线时执行 f←fr。特别地,在 y 轴上行走时不考虑竖线,同时经过横线和竖线时先执行前者。
求最终的 f。记为 euclid(a,b,c,n,u,r)。
其中 a,b≥0,n,c>0。
万能欧几里得算法
分情况考虑。
设 m=⌊can+b⌋。
当 m=0 时,答案为 rn。
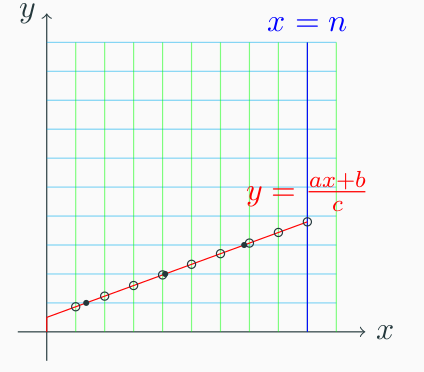
当 b≥c,即 cb≥1 时,在 y 轴上行走的贡献为 u⌊cb⌋,而剩余部分相当于 y=cax+(bmodc) 时的答案,因此答案为 u⌊cb⌋euclid(a,bmodc,c,n,u,r)。
(图片来源于同学课件)
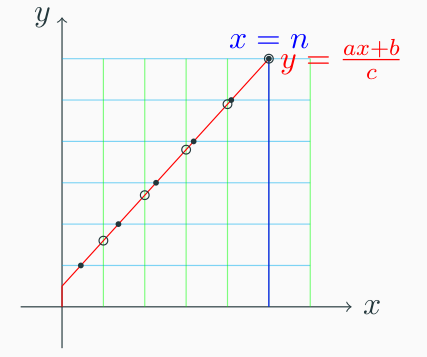
当 a≥c,即 ca≥1 时,任意相邻两个 r 之间至少有一个 u 的贡献,考虑将这个贡献算到 r 上,也就是 r←ur。
此时我们需要改变直线使得相邻两个 r 之间都恰好减少一个 u 的贡献。
可以发现相邻两个 r 之间 u 的贡献的数量是由两个 r 的 y 坐标的差值决定的,因此相当于时相邻两个 r 的 y 坐标的差值都减少 1,相当于斜率减 1。因此直线变为 y=c(a−c)x+b。
重复这个过程即可得到答案为 euclid(amodc,b,c,n,u,u⌊ca⌋r)。
剩余的最后一种情况就是 a<c 且 b<c。考虑将平面沿 y=x 对称。对于同时遇到 u,r 的问题,可以将直线向右平移 c1。
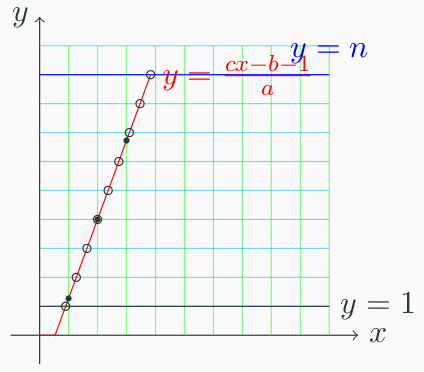
可以把贡献拆成三部分,第一次 u 及以前,中间部分和最后一次 u 之后。
第一部分答案为 r⌊ac−b−1⌋u。
第三部分考虑原直线最后一个 u 的位置为 y=⌊can+b⌋=m,对称后即为 x=m,此时 y=acm−b−1,因此有 n−⌊acm−b−1⌋ 个 r 的贡献,答案为 rn−⌊acm−b−1⌋。
对于第二部分,考虑截掉前两部分,也就是保留 x=m 以前(包含)的部分,然后将直线左移 1,下移 ⌊ac−b−1⌋。
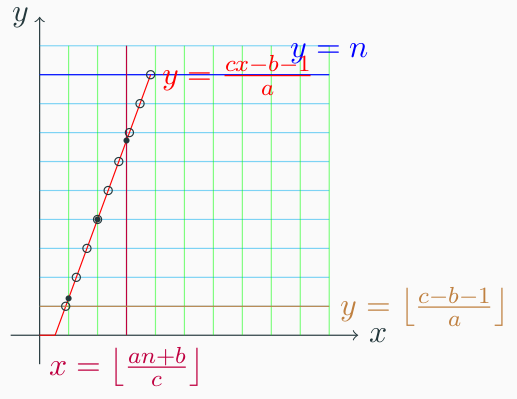
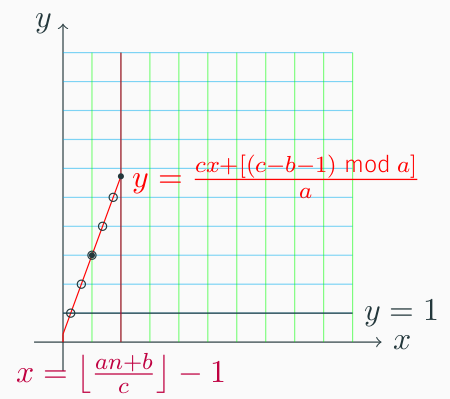
因此这部分答案为 euclid(c,(c−b−1)moda,a,m−1,r,u)。
综合一下即可得到:
euclid(a,b,c,n,u,r)=⎩⎪⎪⎨⎪⎪⎧rnu⌊cb⌋⋅euclid(amodc,bmodc,c,n,u,u⌊ca⌋r)r⌊ac−b−1⌋u⋅euclid(c,(c−b−1)moda,a,m−1,r,u)⋅rn−⌊acm−b−1⌋m=0a≥c∨b≥cotherwise
时间复杂度分析
显然递归 O(loga+logc) 次。
考虑快速幂的复杂度,其中第一种情况为 O(logn),只会出现一次。
第二种情况为 O(logb−logc+loga−logc),但是 O(logb−logc) 部分只会出现至多一次。
第三种情况中 r⌊ac−b−1⌋ 部分是 O(logc−loga),rn−⌊acm−b−1⌋ 部分,cm≥an+b−c,因此 cm−b−1=O(an+b−c−b−1)=O(an−c),因此这里指数是 O(ac) 的,这部分复杂度也是 O(logc−loga)。
第二种和第三种情况会交替出现,上一次的 min{a,c} 即为下一次的 max{a,c},因此总时间复杂度也是 O(loga+logc)。
因此,设一次乘法的复杂度为 O(T),则复杂度为 O(T(loga+logb+logc+logn))。