网络流模板小记

跳过证明，只写做法。

概念

网络（network）是指一张特殊的有向图 $G = (V, E)$。
$E$ 中每条边 $(u, v)$，有一个被称为流量（capacity）的权值，记作 $c(u, v)$。若 $(u, v) \notin E$，则可以认为 $c(u, v) = 0$。
$V$ 中有两个特殊点：源点（source）$s$ 和汇点（sink）$t$。

对于一张网络 $G = (V, E)$，流（flow）定义为一个从边集到整数集或实数集的函数 $f: E \to \mathbb{Z}$ 或 $f: E \to \mathbb{R}$，其满足如下性质：

• 容量限制：对于每条边 $(u, v)$，流经该边的流量不得超过该边的容量，即 $\forall (u, v), 0 \le f(u, v) \le c(u, v)$。
• 流守恒性：除源汇点外，任意点净流量为 $0$，即 $\forall u \ne s \land u \ne t, f(u) = \sum _ {v \in V} f(u, v) - \sum _ {v \in V} f(v, u) = 0$。

定义一个流的流量 $|f|$ 为 $s$ 的净流量 $f(s)$，也等于 $t$ 的净流量的相反数 $-f(t)$。

最大流

最大流问题要求找出一张网络上流量最大的流。

Ford-Fulkerson 增广

对于网络 $G$ 和 $G$ 上的流 $f$，我们定义每条边的剩余容量（Residual Capacity）$c _ f(u, v)$ 为容量与流量之差，即 $c _ f(u, v) = c(u, v) - f(u, v)$。

我们将 $G$ 中结点和剩余容量大于 $0$ 的边构成的图称为残量网络（Residual Network），即 $G = (V, E _ f), E _ f = \{(u, v) \mid c _ f(u, v) > 0\}$。

我们将 $G _ f$ 上一条从源点到汇点的路径称为增广路（Augmenting Path）。对于一条增广路，给每条边都加上一个相等的流量就可以使流量增加，这一过程被称为增广（Augment）。

FF 算法的核心思想就是每次在残量网络上增广直到找不到增广路。

但是直接来是错误的，需要引入“反悔”操作：对于每条边 $(u, v)$，都建一条反向边 $(v, u)$，我们约定 $f(v, u) = -f(u, v)$。这样给一条边增加一定的流量相当于减少这条边的剩余容量并给反向边增加相等的剩余容量，这样每次增广时经过反向边就相当于给这条边“退流”。

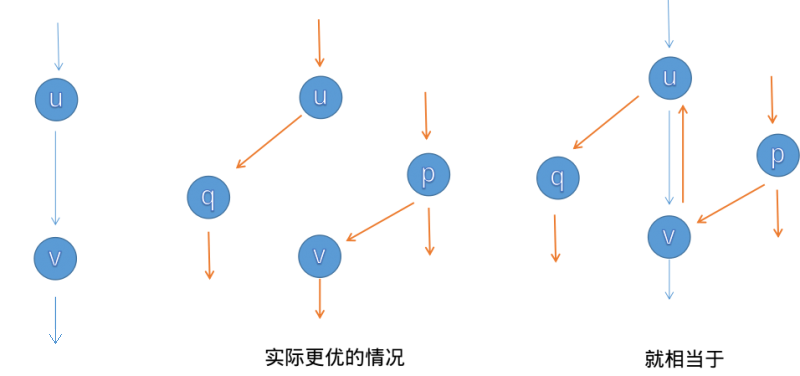
（图源 OI Wiki）

可以证明当 FF 算法无法找到增广路时得到的就是最大流。证明需要下文提到的最大流最小割定理，这里不做展开。

FF 算法的常见实现有 EK、Dinic、SAP、ISAP 等。

Edmonds-Karp 算法

EK 算法的核心思想是每次找到一条增广路，令 $\Delta$ 为增广路上每条边的剩余容量的最小值，然后增广 $\Delta$ 的流量。
该过程可以使用 bfs 实现。

EK 算法会增广 $O(|V||E|)$ 轮，时间复杂度为 $O(|V||E| ^ 2)$。

Dinic 算法

Dinic 算法在增广前先将 $G _ f$ 分层，根据结点 $u$ 到 $s$ 的距离 $d(u)$ 将图分层若干层，只保留满足 $d(u) + 1 = d(v)$ 的边。我们称剩下的部分为 $G _ f$ 的层次图（Level Graph），即 $G _ f$ 的层次图为 $G _ L = (V, E _ L), E _ L = \{(u, v) \mid (u, v) \in E _ f, d(u) + 1 = d(v)\}$。

我们称在 $G _ L$ 上找到的最大流 $f _ b$ 为 $G _ L$ 的阻塞流（Blocking Flow）。

Dinic 算法的流程是每次 bfs 求出 $G _ f$ 的层次图 $G _ L$，然后在 $G _ L$ 上 dfs 求出阻塞流 $f _ b$，将 $f _ b$ 并到原先的流 $f$ 中，直到不存在 $s$ 到 $t$ 的路径。

剩下来的问题是求 $G _ L$ 的阻塞流 $f _ b$。

一个优化是多路增广，即每次增广时不一定需要重新从 $s$ 开始，若当前点还有剩余流量，则从当前点继续增广即可。

另一个优化是当前弧优化，对于一条边 $(u, v)$，若其剩余流量已经为 $0$ 或从 $v$ 无法增广，则我们直接跳过这条边。具体实现时，我们对于每个点 $u$ 维护一个指针 $cur _ u$ 表示第一条还有必要尝试的出边，每次从 $cur _ u$ 开始遍历而不是从头开始遍历出边。

需要注意的是，多路增广只是常数优化，而当前弧优化则保证了时间复杂度。

Dinic 只会增广 $O(|V|)$ 轮，时间复杂度为 $O(|V| ^ 2 |E|)$。

参考代码

最小割

对于一张网络 $G = (V, E)$，我们定义其上的割为一种点集划分方式，其将 $V$ 划分为两个点集 $S, T$，其中 $s \in S, t \in T$。

我们定义割的容量 $c(S, T)$ 为所有从 $S$ 到 $T$ 的边的容量之和，即 $c(S, T) = \sum _ {u \in S, v \in T} c(u, v)$。

最小割问题即为求一张网络的容量最小的割。

最小割最大流定理

对于一张网络，其最小割的容量等于其最大流的流量。

最小费用最大流

对于一张网络 $G = (V, E)$，额外给每条边一个费用表示这条边每流过一单位的流量需要支付的费用，求费用最小的最大流。

SSP 算法

SSP（Successive Shortest Path）算法的核心思想是每次找到单位费用最小的增广路进行增广，并且将反向边的费用设为原边费用的相反数。

SSP 算法无法解决图上有负圈的情况，但是可以证明，若原网络中没有负圈，则增广过程中也不会出现负圈。

实现只需要将 EK 或 Dinic 的 bfs 改成求最短路即可。

若使用 Bellman-Ford 求最短路，则时间复杂度是 $O(|V||E||f|)$ 的，但实际题目中图一般会有一些特殊的性质，所以不能直接用该复杂度来判断算法是否可行。

一个有趣的性质：每次找到的增广路的单位费用是单峰的，因此若用 EK 实现，则可以方便地求出最小费用可行流。

Primal-Dual 原始对偶算法

考虑将费用转化成非负的情况然后使用 dijkstra 求最短路。

具体做法类似于 Johnson，先求出源点到每个点的最短路 $h _ u$，然后对于一条边 $(u, v)$，将其费用 $w$ 改成 $w + h _ u - h _ v$。正确性证明同 Johnson。

然后考虑每次增广后如何更新势能。

结论是设每个点的最短路为 $d' _ u$（该最短路由新权值求出），则 $h _ u \gets h _ u + d' _ u$ 即可。

证明考虑一次增广会使某些边 $(u, v)$ 的反边加入到残量网络中，这些边一定满足 $d' _ u + w + h _ u - h _ v = d' _ v$，即 $-w + (h _ v + d' _ v) - (h _ u + d' _ u) = 0$，因此反边边权非负。
而对于原有的边，其满足 $d' _ u + w + h _ u - h _ v \ge d' _ v$，即 $w + (h _ u + d' _ u) - (h _ v + d' _ v) \ge 0$，因此原边边权也非负。

一般使用 EK 来实现原始对偶算法。

参考代码

上下界网络流

对于每条边给定一个流量下界 $b(u, v)$，需要额外满足 $\forall (u, v), b(u, v) \le f(u, v) \le c(u, v)$。

无源汇上下界可行流

没有源点和汇点，对于所有点满足 $f(u) = 0$，求一个可行的流。

先强制每条边流到流量下界，建立虚拟源汇点 $s, t$，对于每个点 $u$ 考虑此时的净流量：

• $f(u) = 0$：满足条件，不用管。
• $f(u) > 0$：出流大于入流，从 $u$ 向 $t$ 连容量为 $f(u)$ 的边。
• $f(u) < 0$：入流大于出流，从 $s$ 向 $u$ 连容量为 $-f(u)$ 的边。

将原图中每条边的容量设为 $c(u, v) - b(u, v)$，则从 $s$ 到 $t$ 的流相当于增加调整流量的过程。

若 $s$ 的出边流满（等同于 $t$ 的入边流满），则找到了一条可行流。

参考代码

有源汇上下界可行流

连一条 $t$ 到 $s$ 容量正无穷下界为 $0$ 的边，然后跑无源汇上下界可行流即可，流量为新增边的流量。

有源汇上下界最大流

求出可行流后删掉 $t$ 到 $s$ 的边，在残量网络上跑 $s$ 到 $t$ 的最大流，该最大流加上原本的可行流即为答案。

参考代码

有源汇上下界最小流

同理，改成求 $t$ 到 $s$ 的最大流，原可行流减去该最大流即为答案。

参考代码

有源汇上下界最小费用流

做法是一样的，所有新增边费用为 $0$。

需要注意求最小流时需要改成费用最大。

有负圈的最小费用最大流

先钦定所有负圈边流满，即上下界均为流量。然后对于负边建反向、容量相同、费用为相反数的边用于退流原边。

这样就转化成了有源汇上下界最小费用最大流。

参考代码