ICPC 沈阳 2022 B. Binary Substrings 题解

2023-10-28

3.7k 词

问题概述

给你一个正整数 $n$ （ $1 \le n \le 2 \times 10 ^ 5$ ），求一个长度为 $n$ 的 01 串，使得其本质不同的子串数量在所有 $2 ^ n$ 个长度为 $n$ 的 01 串中最多。

答案上界

我们考虑字符串的长度 $i$ ，显然在长度为 $n$ 的字符串中，本质不同的长度为 $i$ 的字符串个数上界为 $\min\left\{2 ^ i, n - i + 1\right\}$ ，所以答案上界为 $\sum _ {i = 1} ^ n \min\left\{2 ^ i, n - i + 1\right\}$ 。

对于 n = 2 ^ k + k - 1

这里我们引入一个名为 De Bruijn Graph 的特殊的有向图。

定义 De Bruijn Graph 为一个有 $k ^ n$ 个点的有向图，每个点为一个由 $k$ 种元素组成的有序 $n$ 元组。当且仅当两个点 $u, v$ 满足，将 $u$ 循环左移一位（即将 $(a _ 1, a _ 2, \ldots, a _ n)$ 变为 $(a _ 2, a _ 3, \ldots, a _ n, a _ 1)$ ）并修改最后一位为任意值可以得到 $v$ 时，存在一条从 $u$ 连向 $v$ 的边权为 $v$ 的最后一位的边。

不妨用 $G(k, n)$ 表示元素种类数和有序组长度分别取 $k$ 和 $n$ 时的 De Bruijn Graph，定义 $G'(n)$ 为 $G(2, n)$ 。

另外定义 De Bruijn Sequence：

De Bruijn Sequence $B(k, n)$ 为一个由 $k$ 种元素组成的循环序列，使得任意由 $k$ 种元素组成的有序 $n$ 元组都是其某个子串且只出现恰好一次。 $B(k, n)$ 的长度为 $k ^ n$ 。

我们发现，当存在 $k$ 使得 $n = 2 ^ k + k - 1$ 时要达到答案上界，必须满足对于 $1 \le i \le k$ ，所有长度为 $i$ 的串都出现至少一次，且对于 $k < i \le n$ ，我们的串中所有长度为 $i$ 的子串互不相同。并且由于 $n - k + 1 = 2 ^ k$ ，所以所有长度为 $k$ 的串都出现恰好一次。

显然的，如果满足最后一个条件，那么前面的条件就都满足了。

我们不妨定义 $B'(n)$ 为满足 $B(2, n)$ 的性质的非循环序列，则当 $n = 2 ^ k + k - 1$ 时 $B'(k)$ 即为我们要求的答案。

同时我们发现，对于 $G'(k)$ 上的一条路径，我们将起点记为一个 01 串，并按顺序在其后接上路径上边的边权，则 $G'(k)$ 上的路径与 01 串形成双射。并且 $G'(k)$ 上的一条哈密顿路径与 $B'(k)$ 一一对应。

于是我们将问题转化成了求 $G'(k)$ 上的任意一条哈密顿路径。

关键性质 1： $G'(k - 1)$ 的欧拉回路与 $G'(k)$ 的哈密顿回路形成双射。

容易发现 $G'(k)$ 上的一个点 $(a _ 1, a _ 2, \ldots a _ k)$ 与 $G'(k - 1)$ 上的一条边 $(a _ 1, a _ 2, \ldots a _ {k - 1}) \to (a _ 2, a _ 3, \ldots a _ k)$ 一一对应，故关键性质 1 正确。

于是我们可以通过求 $G'(k - 1)$ 的欧拉回路得到 $G'(k)$ 的一条哈密顿回路，断开任意一条边即可得到一条哈密顿路径，进而求出 $B'(k)$ ，从而解决 $n = 2 ^ k + k - 1$ 的情况。

另外，马丁（M. A. Martin）在 1934 年证明了可以用一个贪心算法构造出一个合法的 $B(2, n)$ ：先写出 $n$ 个 $0$ 表示序列前 $n$ 项，然后每次尝试添加 $1$ ，若添加 $1$ 可以满足最后的 $n$ 项组成的 $n$ 元组在之前没出现过，则添加 $1$ ，否则添加 $0$ ，直到长度为 $2 ^ n$ 。

我们可以按这种方法构造出 $B(2, k)$ 后再添加 $k - 1$ 个 $0$ 即可得到 $B'(k)$ 。

对于其他情况

我们找到一个 $k$ 使得 $2 ^ k + k - 1 < n < 2 ^ {k + 1} + (k + 1) - 1$ ，则要达到答案上界必须满足对于所有 $1 \le i \le k$ ，所有长度为 $i$ 的串都出现至少一次，且对于所有 $k < i \le n$ ，我们的串中所有长度为 $i$ 的子串互不相同。

显然我们只需要保证所有长度为 $k$ 的串都出现至少一次且我们的串中所有长度为 $k + 1$ 的子串都互不相同即可。

考虑从 $B'(k)$ 扩展。

显然通过上面的任意一种方式构造出来的 $B'(k)$ ，只要在末尾添加一个 $0$ 即可成为 $G'(k)$ 的一条哈密顿回路（使用第一种方法则要求哈密顿路径的起点为 $(0, 0, \ldots, 0)$ ，或者从一开始就不断开边）。不妨设其为 $B''(k)$ 。

同样的转路径为环，我们可以把问题转化成求一个 $G'(k + 1)$ 上的长度为 $n - k$ 的简单环，且每对对应的点（仅首位不同的点）都有至少一个出现在环上。

关键性质 2：对于任意 $a _ 1, a _ 2, \ldots, a _ k$ ，子串 $0, a _ 1, a _ 2, \ldots, a _ k$ 和子串 $1, a _ 1, a _ 2, \ldots, a _ k$ 有且仅有一个在 $B''(k)$ 中出现。

这是显然的，因为对于任意 $a _ 1, a _ 2, \ldots, a _ k$ 都只会出现恰好一次（除了 $B''(k)$ 开头的 $k$ 个，它会在 $B''(k)$ 末尾再出现一次）。

于是 $B''(k)$ 在 $G'(k + 1)$ 上对应一个环。

我们把 $G'(k + 1)$ 上的点分成两部分，一部分第一个元素为 $0$ ，另一部分第一个元素为 $1$ 。

关键性质 3：两个对应的点的出边和入边相同。

为保证路径不经过重复的点，两个对应的点的出边必须不同。而 $B''(k)$ 已经钦定了每对对应的点中某一个的出边，从而确定了另一个点的出边，这样每个点的出边都被确定了，且形成了一个大小为 $2 ^ k$ 的环和其他的一些小环，并且每对对应的点都有恰好一个在大环中。

我们每次找到一对对应的点，使得它们只有一个在大环中，交换它们的出边，即可合并两个环。

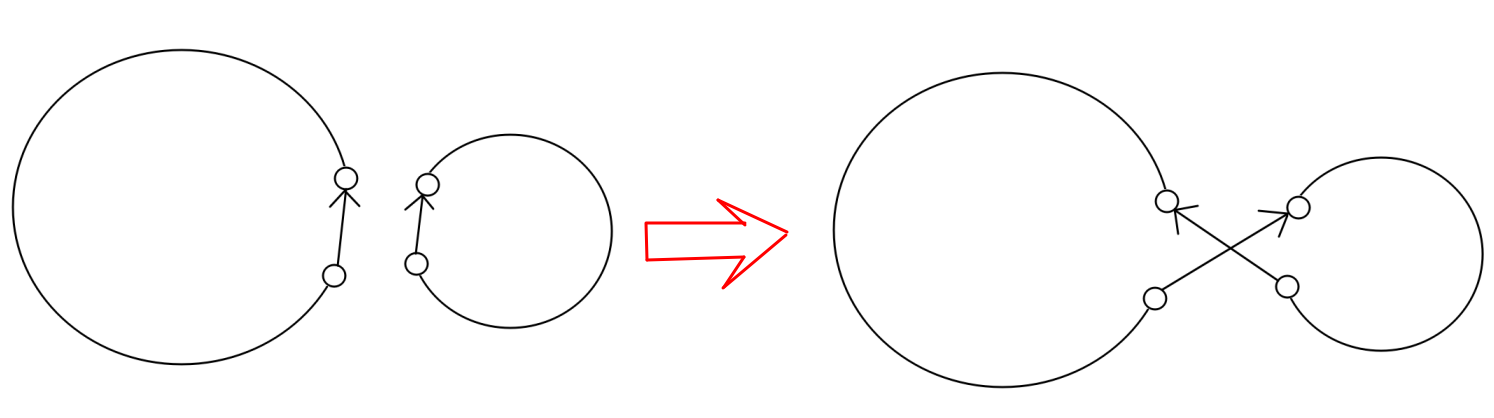
容易发现每次合并后依然是符合要求的。

当大环小于 $n - k$ 时，我们可以任意合并，直到大环大于等于 $n - k$ 。若大环等于 $n - k$ ，则大环即为答案。否则，容易发现最后一次合并后大环还是一个连续的段，于是我们只需要取任意一个包含这次合并前的大环的连续段即可。

总时间复杂度为线性。

对于字符集更大的情况

有空再研究，咕咕咕。

分类

文章目录