字符串乱学

打算系统性地学习和复习一下字符串算法。

一些算法内容比较多会拆到别的文章里。

符号与约定

首先让我们形式化地定义一下字符串的各个概念。

字符集为一个建立了全序关系的集合，用符号 $\Sigma$ 来表示。其中的元素被称为字符。

Tip: 有些时候全序关系不是必须的。

字符串 $s$ 是一个由若干字符按顺序排列而成的序列。

下文默认字符串下标从 $1$ 开始。

定义 $s_i$ 表示字符串 $s$ 的第 $i$ 个字符。

定义 $\left|s\right|$ 为字符串 $s$ 的长度。

空串即为不包含任何字符，$\left|s\right| = 0$ 的字符串。

我们定义字符与字符、字符与字符串、字符串与字符、字符串与字符串之间的拼接表示将这两个字符或字符串按顺序拼在一起得到的字符串，写作 $s + t$ 或 $st$。$s^k$ 表示 $k$ 个 $s$ 拼接。

字符串 $s$ 的一个子串 $s_{[l, r]}$ 表示 $s_l, s_{l + 1}, \ldots s_{r}$ 按顺序连接得到的字符串，即 $s_l + s_{l + 1} + \ldots s_r$。特别地，当 $[l, r] = \varnothing$ 时表示空串。
字符串 $s$ 的一个子序列 是由 $s$ 中的某些字符按原先的顺序拼接得到的字符串。

字符串 $s$ 的后缀为从某个位置 $i$ 开始到 $s$ 的最后一个字符的子串，用 $\mathrm{suf}(s, i)$ 表示，即 $\mathrm{suf}(s, i) = s_{[i, |s|]}$。真后缀为不是其本身的后缀，空串为任意字符串的后缀。
字符串 $s$ 的前缀为从 $s$ 第一个字符开始到某个位置 $i$ 的子串，用 $\mathrm{pre}(s, i)$ 表示，即 $\mathrm{pre}(s, i) = s_{[1, i]}$。空串为任意字符串的前缀。

字典序：以第 $i$ 个字符作为第 $i$ 关键字进行大小比较。若字符串 $s_1$ 为字符串 $s_2$ 的前缀，则认为 $s_1 < s_2$。

回文串（Palindrome String） 为满足 $\forall 1 \le i \le \left|s\right|, s_i = s_{\left|s\right| - i + 1}$ 的字符串。

字典树（Trie）

对于若干个字符串，我们构建出一棵有根树，这棵树有如下性质：

• 每条边上有一个边权，是一个字符。
• 每个点向儿子连的边的边权互不相同。
• 按顺序拼接从根到某个点的路径上的边权，得到的串一定是给出的字符串中某些串的前缀。
• 根到叶子的路径对应的串一定是某个给出的串。

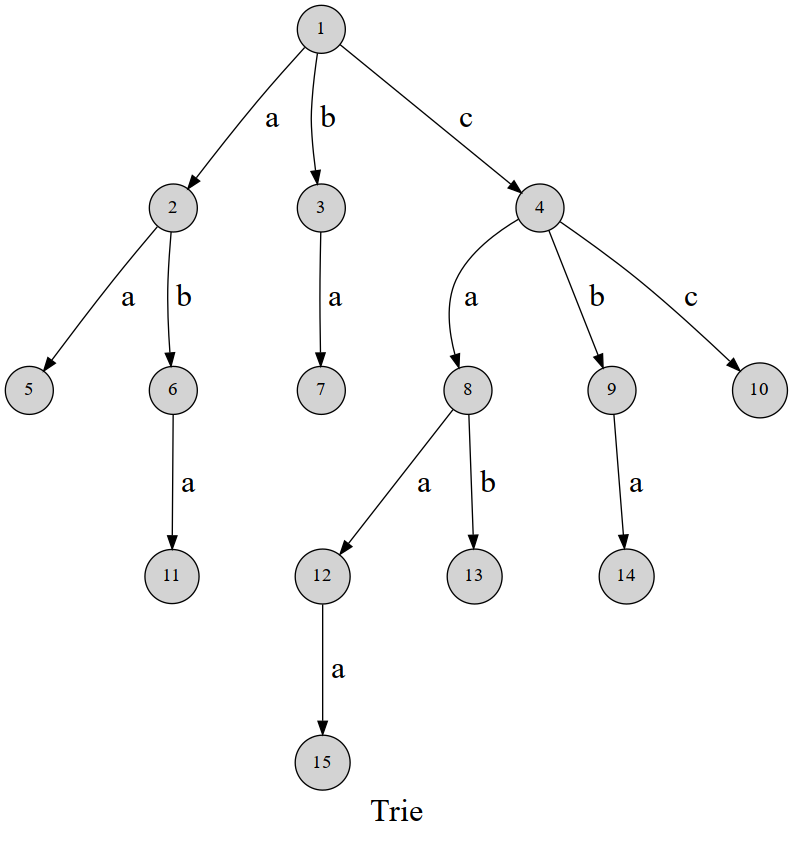
例如：对于字符串 aa，aba，ba，caaa，cab，cba，cc，我们可以构造出如下的树：

（图源 OI Wiki）

这棵树被称为 Trie。

考虑如何构造 Trie。
我们考虑每次插入一个字符串，动态维护 Trie 的形态。

具体地，每次从根开始遍历，并同时维护该字符串当前的字符，如果当前点已经有该字符的儿子，就直接走过去，否则新建一个节点。

void insert(string s) {
	int now = 0;
	for (char c : s) {
		int id = c - 'a';
		if (!trie[now][id]) trie[now][id] = ++tot;
		now = trie[now][id];
	}
	return ;
}

Trie 的大小是 $O(\sum s)$ 的。可以通过合并二度点的方式将大小缩小到 $O(n)$（即压缩 Trie）。

Trie 的基本应用是查询某个串是否在给出的字典中出现过或查询某个串是字典中多少串的前缀。

要实现如上操作需要在每个节点上维护以该点为前缀的串的个数以及该点是否为给出的串。

对 Trie 的先序遍历可以实现字符串排序。

Trie 的本质是一个接受且仅接受给定串的自动机。

可以将整数视为定长的二进制串然后构建 Trie，这种 Trie 被称为 01Trie，由于其拥有非常优秀的树形结构因此常被用来维护与二进制操作相关的信息，由于与字符串关系不大因此这里略去不讲。

例题：[NEERC2016] Binary Code

给定 $n$ 个 01 串，每个串有至多一位是未知的，可以填 0 或 1，求是否存在一种方案，使得任意一个字符串都不是其他串的前缀。若有解则输出方案。

$1 \le n \le 5\times 10^5$，字符串总长不超过 $5\times 10^5$。

TL: 2s, ML: 1GB

考虑两个串 $s_i, s_j$，如果一种填法不合法，相当于要求若 $s_i$ 填了某个字符则 $s_j$ 不能填某个字符。是一个 2-SAT 问题。

问题是如果两两比较连边的话复杂都是 $O(n^2)$ 的，无法接受。

由于是前缀关系，考虑建出 Trie 树。对于每个串，将两种填法都加到 Trie 中，这样两个点之间有边当且仅当他们是祖先关系，发现树边刚好可以满足这点限制，直接拿来用好了。

实际实现时需要注意一些细节。

Border 理论

link

Z 函数（Z Algorithm）

对于一个字符串 $s$，定义函数 $z(i)$ 为 $s$ 与 $\mathrm{suf}(s, i)$ 的最长公共前缀（Longest Common Prefix, LCP）的长度。特别地，$z(1) = 0$。

显然求 Z 函数有一个朴素的 $O(|s|^2)$ 暴力就是枚举每个位置然后暴力向后延伸。考虑优化这个暴力。

假设我们已经求出 $z(1), z(2), \ldots, z(i - 1)$，考虑如何根据这些信息求出 $z(i)$。
我们取出 $j + z(j)$ 最大的一个位置，若 $i < j + z(j)$，可以得到 $s_{[i, j + z(j))} = s_{[i - j + 1, z(j)]}$，因此 $z(i) \ge \min\{z(i - j + 1), j + z(j) - i\}$。
考虑每次以这个作为 $z(i)$ 的初值再暴力向后扩展。

看起来好像只是优化了常数？实际上若 $i \ge j + z(j)$ 或 $j + z(j) - i \le z(i - j + 1)$ 都会使 $j + z(j)$ 增加至少 $1$。而当 $i < j + z(j)$ 且 $j + z(j) - i > z(i - j + 1)$ 时一定有 $z(i) = z(i - j + 1)$，此时不会进行暴力扩展。因此总时间复杂度就是 $O(|s|)$。

参考代码如下：

// n is |s|.
for (int i = 2, j = 0; i <= n; i++) {
	if (i < j + z[j]) z[i] = min(z[i - j + 1], j + z[j] - i);
	while (i + z[i] <= n && s[i + z[i]] == s[1 + z[i]]) z[i]++;
	if (i + z[i] > j + z[j]) j = i;
}

如果你学过 SA 你会发现 Z 函数能求的东西 SA 都能求，所以 Z 函数屁用没有。

Z 函数可以用来加速字符串比较，比较常见的应用是在 DP 中优化时间复杂度，或者纯粹拿来求 LCP。

例题 1：NOIP2020 字符串匹配

给你一个字符串 $s$，求有多少种方式可以将 $s$ 分解成 $(AB)^kC$ 的形式，使得 $A$ 中出现奇数次的字符数不超过 $C$ 中出现奇数次的字符数。

多组数据，$1 \le T \le 5, 1 \le |s| \le 2^{20}$。

TL: 1s, ML: 512MB.

考虑枚举 $|AB|$，此时 $k$ 的取值个数就是 $\lfloor\frac{z(|AB| + 1) + |AB|}{|AB|}\rfloor$。

然后再考虑字符个数的限制，显然我们只要知道 $C$ 中出现奇数次的字符个数就能得到有多少种划分 $AB$ 的方法了。

容易发现 $ABAB$ 的结构对 $C$ 中出现奇数次的字符个数是没有影响的，因此考虑对 $k$ 的奇偶性分类讨论。
当 $k$ 是奇数时，$C$ 中出现奇数次的字符的个数等于 $\mathrm{suf}(s, |AB| + 1)$ 中出现奇数次的字符个数。
当 $k$ 是偶数时，$C$ 中出现奇数次的字符个数等于全串出现奇数次的字符个数。

然后就做完了，时间复杂度 $O(T|s||\Sigma|)$。

例题 2：ARC058F 文字列大好きいろはちゃん

给 $n$ 个字符串，从中选出若干个，按给定顺序拼接，要求总长恰好为 $k$，求字典序最小的串。

$1 \le n \le 2000, 1 \le k \le 10^4$，字符串总长不超过 $10^6$。

TL: 5s, ML: 750MB.

考虑朴素 DP：设 $dp_{i, j}$ 表示前 $i$ 个串总长为 $j$ 时字典序最小的串，直接来时空间都是 $O(nk^2)$ 的。

先对于每个 $i, j$ 求出 $dp_{i, j}$ 有没有可能成为最终答案，即用 $i$ 后面的串能不能拼出 $m - j$ 的长度，然后抛弃掉不能成为答案的状态。
接下来考虑对于 $j < k$，若 $dp_{i, j}$ 不是 $dp_{i, k}$ 的前缀，则较大的那个必然不会成为答案。
这样操作后对于同一个 $i$，所有有效的状态较小的一定是较大的前缀，这样我们对于每个 $i$ 只需要记录最长的一个串即可。

然后考虑转移，按 $j$ 从小到大转移。$dp_{i, j}$ 显然只能从 $dp_{i - 1, j}$ 和 $dp_{i - 1, j - |s_i|}$ 转移过来，比较一下得到 $dp_{i, j}$，然后维护有效的状态。

考虑用一个单调栈维护有效状态，比较当前最长的串和 $dp_{i, j}$：

• 若是 $dp_{i, j}$ 的前缀：直接把 $dp_{i, j}$ 放入栈中。
• 若比 $dp_{i, j}$ 小：$dp_{i, j}$ 无效。
• 若比 $dp_{i, j}$ 大：一直弹栈直到栈顶是 $dp_{i, j}$ 的前缀。

考虑这个过程中我们要支持什么串的比较，显然用到的所有串都是上一轮的最长串的某个前缀接上 $s_i$，将这两个串拼一起求 Z 函数即可实现 $O(1)$ 比大小。

时间复杂度 $O(nk + \sum |s_i|)$。

Manacher

Manacher 用于求一个字符串 $s$ 的所有回文子串，也等价于求每个回文中心对应的最长回文子串的长度。

长度为偶数的回文子串的回文中心是两个字符，比较难搞，考虑用一些方法将它变成长度为奇数的串。

对于字符串 $s = s_1 s_2 s_3 \ldots s_n$，将其变成 $\#s_1\#s_2\#s_3\#\ldots\#s_n\#$，这里 $\#$ 是一个不在 $s$ 字符集中的特殊字符，这样所有长度为偶数的回文子串的中心就变成了某个 $\#$，并且若现在求得的最长回文子串的长度为 $p$，则原串长度就是 $\lfloor\frac{p}{2}\rfloor$，即新串的「半径」。

朴素暴力就是直接来。考虑用类似 Z 函数的方法优化。设 $p_j$ 为以 $j$ 为回文中心的最长回文子串的半径，假设已经求出了 $p_1, p_2, p_3, \ldots, p_{i - 1}$，取 $j + p_j$ 最大的 $j$，若 $i \le j + p_j$，则有 $p_i \ge \min\{p_{2j - i}, j + p_j - i + 1\}$。以此为 $p_i$ 的初值，然后暴力扩展。

时间复杂度分析和 Z 函数类似，读者自证不难，这里不再赘述。

注意实现时一般在两端添加另外两个特殊字符以防止越界。

// t is the original string, n is |t|.
string s = "^#";
for (char i : t) s.push_back(i), s.push_back('#');
s.push_back ('@');
for (int i = 1, j = 0; i <= 2 * n + 1; i++) {
	if (i <= j + p[j]) p[i] = min (p[2 * j - i], j + p[j] - i);
	while (s[i - p[i] - 1] == s[i + p[i] + 1]) p[i]++;
	if (i + p[i] > j + p[j]) j = i;
}

例题：PKUSC2024 Day1T1 回文路径

给定一个 $2\times n$ 的网格，每个格子上有一个字符，你可以从任意格子开始，往右或往下移动，在任意格子结束。记录下经过的格子的字符组成的字符串，求最长的路径长度使得该串是回文串。

$1 \le n \le 10^5$。

TL: 1s, ML: 512MB.

先求出只在某一行的最长回文子串，然后考虑在某个地方拐弯。
不妨假设回文中心在第一行，在回文中心右侧拐弯。

如果拐弯要不劣于不拐弯，那么容易得出如果在 $p$ 处向下拐，则第一行 $p + 1$ 的后缀和第二行 $p$ 的后缀的 LCP 的右端点应当恰好是原回文串的右端点。

容易发现此时等价于在回文串右端点拐弯，因此对于每个原本的回文串，有唯一确定的拐点。之后就直接二分哈希即可。

后缀数组（SA）

咕。

自动机理论初探（Automaton）

尽量在不引入计算理论的情况下解释自动机的用处。因此会讲得比较简略且不太会设计正则语言相关内容。

形式语言

在讲自动机之前，我们需要先了解以下定义：

• 定义一个字母表（alphabet）是一个非空有限集合，用 $\Sigma$ 表示，其中元素被称为符号 / 字符（symbol）。
• 字符串是字母表中的元素构成的有穷序列。特别地，用 $\varepsilon$ 表示空串，它是一个长度为 $0$ 的不包含任何字符的字符串。
• 我们定义两个字符串 $a, b$ 的连接为 $ab$ 表示将 $a$ 和 $b$ 按顺序拼接在一起。
• 记所有长度为 $n$ 的字符串的集合为 $\Sigma ^ n$，特别地，$\Sigma ^ 0 = \{\varepsilon\}$，则还可以定义 $\Sigma ^ * = \bigcup _ {i = 0} ^ \infty \Sigma ^ i$。它包含了所有 $\Sigma$ 能构成的字符串。语言（language）是 $\Sigma ^ *$ 的一个子集。一般用 $L$ 表示。

与 OI 中常见的定义稍有不同。

确定性有限状态自动机

确定性有限状态自动机（Deterministic finite automaton, DFA）可以被形式化地定义为一个五元组 $(\Sigma, Q, q_0, F, \delta)$，其中：

• $\Sigma$ 是字母表。
• $Q$ 是一个有限的状态集合。
• $q_0 \in Q$ 是起始状态。
• $F \subseteq Q$ 是接受状态的集合。
• $\delta: Q \times \Sigma \to Q$ 是转移函数。

若将状态看作点，转移函数看作有向边，则可以直观地将一个自动机画成一张状态图。在状态图中，一般用一个没有起点的箭头指向起始状态，用同心圆表示终止状态。

对于一个字符串 $s = s_1s_2\ldots s_n$ 和一个自动机 $M = (\Sigma, Q, q_0, F, \delta)$，如果存在一个状态序列 $r_0, r_1, \ldots, r_n$，使得：

• $r_0 = q_0$
• $\forall 1 \le i \le n, \delta(r_{i - 1}, s_i) = r_i$
• $r_n \in F$

则称这个自动机可以接受该字符串。

对于自动机 $M$，令所有 $M$ 可以接受的字符串的集合为 $L(M)$，则称 $M$ 识别 $L(M)$ 这个语言。

如果一个语言可以被一个 DFA 识别，则称这个语言为正则语言。

非确定性有限状态自动机

与 DFA 类似，非确定性有限状态自动机（Non-deterministic Finite Automaton, NFA）也可以被形式化地定义为一个五元组 $(\Sigma, Q, q_0, F, \delta)$：

• $\Sigma$ 是字母表。
• $Q$ 是一个有限的状态集合。
• $q_0 \in Q$ 是起始状态。
• $F \subseteq Q$ 是接受状态的集合。
• $\delta: Q \times \Sigma \to 2^Q$ 是转移函数。

与 DFA 唯一不同的地方在于转移函数。

NFA 可以接受一个字符串的条件也与 DFA 类似，只需把第二条改为 $r_i \in \delta(r_{i - 1}, s_i)$ 即可。

NFA-$\varepsilon$（带 $\varepsilon$ 移动的 NFA）是一种扩展的 NFA，它允许使用空的符号进行转移。他的转移函数为 $\delta: Q \times \Sigma \cup \{\varepsilon\} \to 2^Q$。也就是在某个状态 $u$ 可以转移到 $\delta(u, \varepsilon)$ 中的某个状态而不消耗任何符号，也就是可以视为在字符串中任意位置可以插入任意个 $\varepsilon$。

看起来 NFA 相较 DFA 能识别更多的语言，NFA-$\varepsilon$ 相较 NFA 也能识别更多的语言，但事实上这三个东西是等价的。

Tip: 称两个自动机等价，当且仅当它们能识别的语言相同。

定理 1：对于任意一个 NFA-$\varepsilon$，都可以找到一个等价的 NFA。

对于 NFA-$\varepsilon$ 上的每个状态，求出其只通过 $\varepsilon$ 转移能到的状态，然后将每个转移变成这些状态的转移的并即可。

更形式化地说就是，对于原 NFA-$\varepsilon$ 中的任意一个状态 $q$ 和任意一个字符 $c$，构造新 NFA 中的状态转移函数为：

$$\delta'(q, c) = \delta(q, c) \cup \delta(\delta(q, \varepsilon), c) \cup \delta(\delta(\delta(q, \varepsilon), \varepsilon), c) \cup \cdots$$

即可。

定理 2：对于任意一个 NFA，都可以找到一个等价的 DFA。

将 NFA 转化成 DFA 的算法被称为子集构造法。

算法实现流程如下：

1. 将初始状态加入到 DFA 中但不标记。
2. 每次取出 DFA 中一个未被标记的状态，加上标记。
3. 将其转移设为其对应的 NFA 中的状态集合的转移的并对应的状态。
4. 若某个转移到的状态未被加入则加入 DFA 但不标记。
5. 重复 2 到 4 步直到所有状态都被标记。

正确性显然。但是这样构造出来的 DFA 的状态数是指数级别的。

因此如果要判断一个串能否被一个 NFA 识别，如果直接将其转化成 DFA 则复杂度会变成指数级。

一种简单的实现方式是转移时记录所有可能到达的状态，这样单次转移复杂度是状态数平方级别的。

显然可以通过 bitset 优化转移。

另外还可以使用四毛子来优化。将 NFA 的状态分块，设大小为 $T$。对于每个块，枚举所有 $2^T$ 种子集，再枚举所有字符，处理出每个子集用每个字符转移到的状态集合，就可以实现快速转移。

分析一下复杂度，是 $O(\frac{|Q|^2 2^T |\Sigma|}{T \omega} + \frac{n |Q|^2}{T \omega})$。取 $T = \log \frac{n}{|\Sigma|}$ 即可得到 $O(\frac{n |Q|^2}{\omega \log\frac{n}{|\Sigma|}})$ 的复杂度。

DFA 最小化

将一个 DFA 转化为与它等价且状态数最少的 DFA，使用 Hopcroft 算法。

首先去除所有无法从 $q_0$ 到达的和无法到达 $F$ 的状态。

我们定义两个状态 $u, v$ 是不可区分的，当且仅当：

• $[u \in F] = [v \in F]$，且
• $\forall c \in \Sigma$，$\delta(u, c)$ 与 $\delta(v, c)$ 相同或不可区分。

Hopcroft 的基本思想是先将所有状态按是否是接受状态划分成两个等价类，然后每次取出一个等价类 $S$，使得存在 $u, v \in S, c \in \Sigma$，$\delta(u, c)$ 和 $\delta(v, c)$ 不在同一个等价类中，然后按转移函数划分 $S$，直到找不到这样的 $S$ 为止。

这样操作后将所有等价类作为新 DFA 的一个状态即可。显然这个 DFA 中不存在两个不可区分的状态。可以证明不存在不可区分的状态的 DFA 是最小的。证明可以参考：https://zh.wikipedia.org/wiki/迈希尔-尼罗德定理。

直接实现应该是平方还立方的，太慢了。一种优化方式是：

维护一个集合表示还没被考虑过的等价类的集合 $W$。每次从中取出一个等价类 $X$，然后枚举字符 $c$ 和有到它的转移的等价类 $Y$，如果可以划分，就按 $c$ 转移是否到 $X$ 划分为两个等价类 $A, B$。然后如果 $Y$ 还没被考虑过则将 $A, B$ 都放入 $W$ 中，否则只将大小较小的那个放入 $W$ 中。

为什么只需要放入小的那个？不妨假设放入的是 $A$，考虑反正，如果存在某个等价类只能被 $B$ 划分，由于已经考虑过 $Y$，因此该等价类中所有状态必然所有转移都能转移到 $Y$，且即存在到 $B$ 的转移又存在到 $A$ 的转移，因此它也能被 $A$ 划分。

这样的时间复杂度就是 $O(|\Sigma||Q| \log |Q|)$。

自动机在 OI 中的应用

可以构造 DFA 以识别某些特定的语言。

例题：CF1142D Foreigner

定义一个数 $x$ 是牛的当且仅当：

• $x$ 是 $1, 2, 3, 4, 5, 6, 7, 8, 9$，或
• $\lfloor\frac{x}{10}\rfloor$ 是牛的，并且将所有牛的数从小到大排序后，$\lfloor\frac{x}{10}\rfloor$ 的排名 $k$（排名从 $1$ 开始）满足 $x \bmod 10 < k \bmod 11$。

给你一个由数码构成的字符串 $s$，求有多少子串不含前导零且对应的数是牛的。

$1 \le |s| \le 10^5$。

TL: 1s, ML: 256MB.

观察条件，可以发现除 $1\sim 9$ 以外的牛的数都能由其他牛的数在末尾添加一个数码得到。

具体地，若一个牛的数 $x$ 的排名为 $k$，则它能生成 $10x \sim 10x + k \bmod 11 - 1$。设 $x' = 10x + c (0 \le c < k \bmod 11)$，$x'$ 的排名 $k'$ 可以方便地用以下式子求出：

$$k' = 9 + \sum\limits_{i = 1}^{k - 1} (i \bmod 11) + c + 1$$

观察发现：

$$0 + 1 + 2 + \ldots + 10 = 55 \equiv 0 \pmod{11}$$

所以我们只需要知道 $k \bmod 11$ 的值即可。

基于这点，我们可以构造一个只接受牛的数的 DFA：

$$\left\{ \begin{aligned} & \Sigma = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\} \\ & Q = \{q_0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} \\ & F = Q \setminus \{q_0\} \\ & \delta(u, c) = \begin{cases} c & u = s, c \ne 0 \\ (10 + \sum_{i = 0}^{u - 1} i + c) \bmod 11 & u \ne s, c < u \end{cases} \end{aligned} \right.$$

设 $dp_{i, u}$ 表示只考虑 $s$ 的长度为 $i$ 的前缀的后缀的串，在 DFA 上的状态为 $u$ 时的方案数，可以容易地写出转移方程。

最终答案即为 $\sum_{i = 1}^{|s|} \sum_{u = 0}^{10} dp_{i, u}$。

另一个应用是 DP 套 DP。对于一个 DP，可以将其 DP 状态视为自动机的状态，把 DP 变成一个自动机的形式。这样在计数满足某些限制条件的串时，就可以先设计一个用来判断串是否满足条件的 DP，然后在由这个 DP 构造的自动机上计数。

实际上就是将上面的手动构造自动机变成了用 DP 状态来表示自动机。

例题：「TJOI2018」游园会

给你一个长度为 $k$，字符集为 $\{\texttt{N}, \texttt{O}, \texttt{I}\}$ 的串 $t$，求长度为 $n$，字符集为 $\{\texttt{N}, \texttt{O}, \texttt{I}\}$ 的串 $s$ 的数量，满足 $s$ 与 $t$ 的 LCS 为 $i$，且不存在一个子串为 $\texttt{NOI}$。
对于所有的 $i$ 求解。

$1 \le n \le 1000, 1 \le k \le 15$。

TL: 6s, ML: 250MB.

设要满足 LCS 为 $m$。

考虑对于确定串计算 LCS：$f_{i, j} = \max\{f_{i - 1, j}, f_{i, j - 1}, f_{i - 1, j - 1} + [s_i = t_j]\}$。

这个串合法当且仅当 $f_{n, k} = m$。

我们以 $f_{i, 1\ldots k}$ 为状态，每次添加一个 $s$ 中的字符进行转移，所有 $f_k = m$ 的状态为接受状态，这样就建出了只能接受与 $t$ 的 LCS 为 $m$ 的自动机。

记 $dp_{i, s}$ 表示前 $i$ 个字符，走到状态 $s$ 的方案数，转移是方便的。

唯一的问题就是自动机的状态数太多。观察上面的 DP 方程，容易发现 $f_j$ 单调不降且相邻两位最多差 $1$，将其差分后容易发现有效状态只有 $2^k$，这样就可以保证复杂度。

注意，某些 DP 套 DP 题的自动机状态数可能会比较大，此时需要用 DFA 最小化算法减少状态数。

常见自动机

子序列自动机

子序列自动机是一个只能接受某个字符串 $s$ 的子序列的自动机。

考虑设 $0$ 为起始状态，令状态 $i$ 表示 $\mathrm{pre}(s, i)$ 的子序列与 $\mathrm{pre}(s, i - 1)$ 的子序列的差集，也就是所有能转移到 $i$ 的字符串其第一次在 $s$ 中出现结尾是 $i$，那么我们这样构造子序列自动机：

$$\left\{ \begin{aligned} & Q = \{x \in \mathbb{N} \mid 0 \le x \le |s|\} \\ & q_0 = 0 \\ & F = Q \\ & \delta(u, c) = \min\{i \mid i > u, s_i = c\} \end{aligned} \right.$$

具体构建时，只需要从后往前遍历，维护每个字符的最后一次出现的位置即可。时间复杂度为 $O(|s||\Sigma|)$。

这样构建出来的子序列自动机满足每个子序列在自动机上经过的点对应其在原串上第一次出现的位置。

KMP 自动机

KMP 是一个接受所有以模式串 $s$ 为后缀的字符串的自动机。

具体来说就是考虑 KMP 匹配的过程，然后建成自动机：

$$\left\{ \begin{aligned} & Q = \{x \in \mathbb{N} \mid 0 \le x \le |s|\} \\ & q_0 = 0 \\ & F = \{|s|\} \\ & \delta(u, c) = \begin{cases} u + 1 & u < |s| \land s_{u + 1} = c \\ \delta(\pi_u, c) & u = |s| \lor (u > 0 \land s_{u + 1} \ne c) \\ 0 & u = 0 \land s_{u + 1} \ne c \end{cases} \end{aligned} \right.$$

构建考虑从前往后加字符，发现若当前长度为 $n$，添加一个字符 $c$ 后有 $\pi_{n + 1} = \delta(n, c)$，因此可以 $O(1)$ 算出前缀函数，所以可以 $O(|s||\Sigma|)$ 构建。

例题：CF1721E Prefix Function Queries

给定一个字符串 $s$ 和 $q$ 个字符串 $t_i$，对于每个 $i$ 求 $s + t_i$ 的最靠后 $|t_i|$ 个前缀的最长 Border 的长度。

$1 \le |s| \le 10^6, 1 \le q \le 10^5, 1 \le |t_i| \le 10$。

TL: 2s, ML: 250MB.

KMP 自动机，每次从 $|s|$ 处重新往后建即可。

KMP 自动机的主要优势在于复杂度不基于均摊，因此可以支持一些可持久化操作等均摊复杂度错误的东西。

AC 自动机（Aho-Corasick Automaton, ACAM）

一组模式串的 AC 自动机是一个接受所有以某个模式串为后缀的串的自动机。

看起来是 KMP 自动机的强化版，考虑用类似的思路去构建。

首先对于模式串建出 Trie。令 $Q$ 为 Trie 上所有节点，$q_0$ 为 Trie 的根，$F$ 为所有模式串对应的节点，然后类似于 KMP 的前缀函数，定义 $fail_i$ 表示 Trie 上 $i$ 表示的串的出现过的最长真后缀对应的点（称其为 fail 指针）。

若我们可以求出 fail 指针，则可以得到其转移函数：

$$\delta(u, c) = \begin{cases} trie_{u, c} & trie_{u, c} = \mathrm{null} \\ \delta(fail_u, c) & u \ne q_0 \land trie_{u, c} = \mathrm{null} \\ q_0 & trie_{u, c} = \mathrm{null} \end{cases}$$

这里 $trie_{u, c}$ 表示 Trie 上节点 $u$ 通过字符 $c$ 走到的儿子，若不存在则令其等于 $\mathrm{null}$。

现在的问题就是怎么求 fail。

与 KMP 自动机类似，可以发现 $fail_{trie_{u, c}} = \delta(fail_u, c)$。因此考虑同时求出 fail 指针和转移函数，这就要求我们规划一个合理的求解顺序。

容易发现 $fail_u$ 的深度一定严格小于 $u$ 的深度，因此从 Trie 的根开始 bfs 即可。

令 $n$ 为 Trie 的大小，$m$ 为字符串总长度，则时间复杂度为 $O(m + n|\Sigma|)$。

参考代码：

struct ACAM {
	int tot, fail[200005], delta[200005][26];

	void insert(string s, int id) {
		int now = 0;
		for (char c : s) {
			int v = c - 'a';
			if (!delta[now][v]) delta[now][v] = ++tot;
			now = delta[now][v];
		}
		return ;
	}
	void build() {
		queue<int> q;
		for (int c = 0; c < 26; c++)
			if (delta[0][c]) q.push(delta[0][c]);
		while (!q.empty()) {
			int now = q.front();
			q.pop();
			for (int c = 0; c < 26; c++)
				if (delta[now][c]) fail[delta[now][c]] = delta[fail[now]][c], q.push(delta[now][c]);
				else delta[now][c] = delta[fail[now]][c];
		}
		return ;
	}
} ac;

对于 AC 自动机上每个点 $u \ne q_0$，连一条 $u$ 到 $fail_u$ 的边，就形成了一棵以 $q_0$ 为根的内向树，被称为 fail 树。

fail 树上每个点的父亲都是该串的最长真后缀，是一个比较优秀的性质，很多题目可以将问题放在 fail 树上考虑然后变成树上问题。

例如：AC 自动机的一个经典应用——多模式串字符串匹配：给你一个文本串和若干模式串，求出每个模式串在文本串中的出现次数。

首先对模式串建出 AC 自动机，然后用文本串在自动机上跑。任意时刻，当前节点及其所有在 fail 树上的祖先对应的串都是当前扫到的文本串的后缀。也就是说每次走到一个节点 $u$，所有 $u$ 的祖先的答案都会增加 $1$。因此在遍历时对每个点单点修改最后求子树和即可。

例题 1：CCPC 2021 Guilin H. Popcount Words

定义 $w(l, r) = s_l s_{l + 1} \ldots s_r$，其中 $s_i$ 是一个字符，其值为 $\mathrm{popcount}(i) \bmod 2$。

给定 $n$ 个区间 $[l_i, r_i]$，然后构造字符串 $S$：

$$S = w(l_1, r_1) + w(l_2, r_2) + \cdots + w(l_n, r_n)$$

$q$ 次询问，每次询问给定一个 01 串 $p$，问 $p$ 在 $S$ 中出现了几次。

$1 \le n, q \le 10^5, 1 \le l_i \le r_i \le 10^9, \sum |p| \le 5\times 10^5$。

TL: 1s, ML: 512MB.

$\mathrm{popcount}(i) \bmod 2$ 形成的序列：

$$\{0, 1, 1, 0, 1, 0, 0, 1, \ldots\}$$

这个序列有个名字叫 Thue-Morse 序列。有一些比较显然的性质：

• 可以按如下方式倍增构造：
  初始时序列为 $\{0\}$，每次将序列复制一遍，并翻转每一位后接到末尾。
  即：$\{0\} \to \{0, 1\} \to \{0, 1, 1, 0\} \to \cdots$。
• 取出其任意一个长度为 $k$ 的子区间，可以将其划分成 $O(\log k)$ 个长度为 $2$ 的次幂的区间，使得每个区间要么是原串的一个前缀，要么可以通过对原串的一个前缀翻转每一位得到。以下用 $T_{i, 0 / 1}$ 表示 Thue-Morse 序列长度为 $2^i$ 的前缀 / 长度为 $2^i$ 的前缀翻转每一位后的结果。

基于这些性质，我们首先可以把 $S$ 拆成 $O(n\log n)$ 段。

对询问串建出 AC 自动机，然后设 $f_{i, j, 0 / 1}$ 表示从 AC 自动机的状态 $i$ 出发，用 $T_{j, 0 / 1}$ 在上面跑，最终走到的状态。$f$ 可以通过 DP 快速得到。

然后在 AC 自动机上跑 $S$，记录 $g_{i, j, 0 / 1}$ 表示从状态 $i$ 出发，用 $T_{j, 0 / 1}$ 在上面跑的次数。也就是对于拆出来的 $O(n\log n)$ 段，只在每段的开头记录信息。

然后从大到小枚举 $j$，对于每个 $g_{i, j, 0 / 1}$，将其贡献拆到 $g_{i, j - 1, 0 / 1}, g_{to_{i, j - 1, 0 / 1}, j - 1, 1 / 0}$ 上。

最后拆到 $j = 0$ 时，就统计出了 AC 自动机上每个转移被经过的次数，然后就可以求出答案了。

例题 2：洛谷 P8147 [JRKSJ R4] Salieri

给出 $n$ 个字符串 $s_i$，每个字符串有一个权值 $v_i$。$m$ 次询问每次给出一个字符串 $S$ 和一个常数 $k$。设 $cnt_i$ 为 $s_i$ 在 $S$ 中的出现次数，求 $cnt_i\times v_i$ 第 $k$ 大的值。

$1 \le n, m \le 10^5, \sum_{i = 1}^n |s_i| \le 5 \times 10^5, \sum |S| \le 5 \times 10^5$。

TL: 2s, ML: 256MB.

考虑二分答案，然后变成求 $cnt_i\times v_i \ge lim$ 的个数。

先对 $s_i$ 建 AC 自动机，然后 $cnt_i$ 就变成了子树和。

显然在 AC 自动机上经过的点的个数为 $|S|$，对这些点建虚树，然后你会发现虚树上每条边的 $cnt_i$ 都相同。问题转化成查询对虚树上每条边（原树上的一条直链）查询 $cnt \times w_i \ge lim \iff w_i \ge \lceil\frac{lim}{cnt}\rceil$ 的个数。用主席树维护即可。

例题 3：The 2020 ICPC Asia Macau Regional Contest B. Boring Problem

给 $n$ 个字符集为前 $k$ 个小写字母长度为 $m$ 的字符串 $t_i$，以及长度为 $k$ 的序列 $p_i$ 满足 $\sum_{i = 1}^k p_i = 1$。

对于一个字符集为前 $k$ 个小写字母的字符串 $S$，进行以下操作：

• 若存在一个串 $t_i$ 是 $S$ 的子串，则操作结束。否则执行下面第二条操作。
• 以 $p_i$ 的概率选择第 $i$ 个字母，将它加到 $S$ 的末尾，然后返回上面第一条操作。

定义 $f(S, t, p)$ 为上述操作结束时 $S$ 的期望长度。给你一个串 $R$，对于每一个 $1 \le i \le |R|$，求 $f(\mathrm{pre}(R, i), t, p)$。对 $10^9 + 7$ 取模。

$1 \le n \le 100, 1 \le n\times m \le 10^4, 1 \le k \le 26, 1 \le |R| \le 10^4$。

TL: 1s, ML: 512MB.

考虑建出 AC 自动机，问题就是对于 AC 自动机求从某个点出发随机游走到接受状态的期望步数。

直接高斯消元是 $O(n^3 m^3 + |R|)$ 的，考虑优化。

注意到 AC 自动机的 Trie 上只有 $n$ 个叶子，以及每个点的转移要么是到儿子，要么是到更浅的点。

于是考虑能否只设出 $n$ 个未知量。对于一个点 $u$，如果只有一个儿子，那儿子的答案就可以直接用 $u$ 的答案描述，否则考虑随便钦定一个重儿子，然后重儿子就可以用 $u$ 和 $u$ 的其他儿子的答案来描述。

因此直接 bfs，只需要设出轻儿子和根总共 $n$ 个未知量，然后根据叶子的答案是 $0$ 就可以得到 $n$ 个方程，高斯消元即可。复杂度为 $O(n^3 + n^2m + |R|)$。

回文自动机 / 回文树（Palindromic Tree）

回文树是一个用来维护某个串上所有回文子串的结构，因为拥有自动机结构又被称为回文自动机（Palindromic Automaton）。

显然自动机是无法识别“回文串”这种非正则语言的，即使是一个串的回文子串这种有限的语言，想要处理也比较有难度。因此我们不妨暂时抛开“自动机”而是先去考虑“树”这个结构。

考虑回文串的定义，维护整个串似乎过于麻烦且信息冗余，不妨对于每个串只维护其右半部分。我们定义一个回文串从回文中心开始的后缀为这个回文串的半串。那么，我们可以简单地将回文树描述成这些回文子串的半串的 Trie。

但是这又涉及在 Manacher 时遇到的问题：回文串的长度有奇数和偶数。一种解决方法是像 Manacher 一样在相邻两个字符之间插入 #，但是这种方法太过丑陋。更好的方法是直接建两棵树，一棵树中所有节点对应的回文串长度均为奇数，另一棵均为偶数。两棵树的根分别被称为奇根和偶根，我们认为它们分别代表长度为 $-1$ 和 $0$ 的空串，这样每个点的父亲的长度就是它的长度 $- 2$。

---

了解完定义后考虑怎么构建 PAM。

与 AC 自动机类似，我们定义节点 $u$ 的 fail 指针指向最长的是 $u$ 对应回文串后缀的回文串对应的节点。特别地，偶根的 fail 指针指向奇根，而我们并不关心奇根的 fail 指针。

考虑增量构造，假设已经构建了 $\mathrm{pre}(s, p - 1)$ 的 PAM，要在当前串末尾加一个字符 $s_p$。

我们考虑从以上一个字符结尾的最长回文子串出发，一直跳 fail，直到当前节点的长度 $len$ 满足 $s_{p - len - 1} = s_p$，这样就找到了新点在 Trie 上的父亲，不妨用 $A$ 表示。

然后如果 $A$ 不存在 $s_p$ 的转移边，就需要新建一个节点，并求新节点的 fail。根据定义，只需要从 $A$ 开始一直跳 fail 直到走到一个存在 $s_p$ 转移的祖先就好了。如果找不到，就将它的 fail 指针设为偶根。这是符合直觉的，因为空串是所有串的后缀。

（图源 OI-Wiki，据说是原论文的图。）

但是先别急，看起来好像每次只增加了以新的字符结尾的最长回文后缀，而没有维护更短的回文后缀。实际上，更短的回文后缀一定出现在之前的串中，因为他被更长的回文串包含，对称一下就对称到前面去了。这同时也说明了一个字符串的本质不同回文子串至多只有长度个，因此其 PAM 的状态数也是线性的。

考虑分析这个东西的复杂度。考虑当前节点在 fail 树上的深度，每次往上跳深度 $-1$，而新增节点深度只会增加至多 $2$（当且仅当跳到奇根时 $+2$，其他情况 $+1$），因此时间复杂度也是均摊线性的。

参考代码：

struct PAM {
	int tot, delta[500005][26], len[500005], fail[500005];
	string s;
	int lst;

	PAM() {tot = 1; len[0] = 0; len[1] = -1; fail[0] = fail[1] = 1;}
	int getfail(int now, int i) {
		while (s[i - len[now] - 1] != s[i]) now = fail[now];
		return now;
	}
	void insert(int i) {
		int now = getfail(lst, i);
		if (!delta[now][s[i] - 'a']) {
			len[++tot] = len[now] + 2;
			fail[tot] = delta[getfail(fail[now], i)][s[i] - 'a'];
			delta[now][s[i] - 'a'] = tot;
		}
		lst = delta[now][s[i] - 'a'];
		return ;
	}
} p;

上面说过，虽然 PAM 长得不那么自动机，但在一定程度上也具有自动机结构。我们可以将它的转移视为在当前字符串的两侧都添加一个相同的字符。

考虑这样一个问题：给定两个串 $s, t$，求它们的公共回文子串。

我们对 $s$ 建出 PAM，然后用 $t$ 在上面跑。具体地，我们从偶根出发，每次尝试转移时判断在 $t$ 上前后两个字符是否相同，如果不同或不存在这个转移就跳 fail 指针。容易证明复杂度也是均摊线性的。

例题 1：洛谷 P4762 [CERC2014] Virus synthesis

初始有一个空串，利用下面的操作构造给定串 $S$ 。

1. 串开头或末尾加一个字符
2. 串开头或末尾加一个该串的逆串

求最小化操作数。

$|S| \le 10^5$。

TL: 1s~10s, ML: 125MB.

考虑最后一次 2 操作，操作完后会变成一个偶回文串，然后剩下的用 $1$ 操作补完，因此只需要求出所有长度为偶数的回文子串的答案即可。

另一个比较重要的观察是所有偶回文的最后一次操作一定是 $2$ 操作。

对 $S$ 建 PAM，设 $f_u$ 为 $u$ 节点的答案，则：

$$\begin{aligned} f_u &\gets \min_{v \text{ 是 } u \text{ 的半串的子串}} f_v + \frac{|u|}{2} - |v| + 1 \\ f_u &\gets f_{fa_u} + 1 \end{aligned}$$

第一个转移是先拼半串的一个子串再补完半串，然后用 $2$ 操作。第二个转移是在拼父亲的串的操作中，在最后一次用 $2$ 操作前先在后面接一个字符。

优化转移是简单的，第一个转移的条件显然可以变成 $v$ 是 $u$ 半串的后缀，这样可以转移过来的 $v$ 就是失配树上一条从根开始的直链。然后直链的底部可以通过父亲的答案快速得到。

例题 2：BZOJ3103 Palindromic Equivalence

给一个字符串 $s$，求合法的字符串 $t$ 的数量，使得 $|t| = |s|$，且 $t$ 中一个子串是回文串当且仅当 $s$ 中这个位置的子串是回文串。

$|s| \le 10^6$。

TL: 435ms, ML: 128MB.

考虑怎么样的串是满足条件的，发现建出 PAM，如果两个串的 PAM 同构且每个点所在的位置相同则符合条件。于是有一个直接的想法就是对 $s$ 建 PAM，然后对于值要相同的位置连一条零类边，要不同的位置连一条一类边，则只要零类边连接的两个点相同，一类边连接的两个点不同即可。

考虑用零类边缩成若干个等价类，然后变成给一张图每个点染色使得相邻点颜色不同。这个显然不可做，于是考虑着一些性质。

大胆猜一下是弦图并且有一个比较阳间的完美消除序列，比如按等价类内最小值从大到小排序。如果猜想正确的话只要从前往后扫一遍直接数就对了。

然后你发现猜对了，考虑怎么证明。

首先你要注意到连边的本质是对于每个极长回文子串 $[l, r]$，将 $l + i, r - i$ 缩等价类，然后给 $l - 1, r + 1$ 连边。

以下用 $E_0, E_1$ 分别表示零类边和一类边构成的集合。

引理一：对于 $i < j < k$，如果 $(i, k), (j, k) \in E_1$，则要么 $i, j$ 在同一等价类，要么 $i, j$ 所在等价类有边。

考虑有回文子串 $s_{[i + 1, k - 1]}, s_{[j + 1, k - 1]}$，则也有回文子串 $s_{[i + 1, i + k - j - 1]}$，且 $(j, i + k - j) \in E_0$，因此如果不满足 $(i, j) \in E_0$ 则 $(i, i + k - j) \in E_1$，即 $i, j$ 所在等价类有边。

引理二：对于同一等价类内的相邻的两个点 $i, j$，一定满足 $(i, j) \in E_0$，即 $s_{[i, j]}$ 是回文串。相邻指按编号从小到大排序后相邻。

考虑对于 $i < j < k$，满足 $s_{[i, k]}, s_{[j, k]}$ 是回文串，则：

• 若 $j = \frac{i + k}{2}$，则 $s_{[i, j]}$ 是回文串。
• 若 $j > \frac{i + k}{2}$，则有回文串 $s_{[i, i + k - j]}$，然后可以得到 $s_{[i + k - j, j]}$ 也是回文串，此时有 $(i, i + k - j), (i + k - j, j) \in E_0$。
• 若 $j < \frac{i + k}{2}$，则有回文串 $s_{[i, i + k - j]}$，然后可以得到 $s_{[j, i + k - j]}$ 也是回文串，变成了 $k - j$ 更小的情况。

对于 $i < j < k$，满足 $s_{[i, k]}, s_{[i, j]}$ 是回文串的情况同理。

因此，对于等价类内任意相邻两个点之间的路径 $p_1, p_2, \ldots, p_n$，对于任意 $p_i < p_{i + 1} > p_{i + 2}$ 或 $p_i > p_{i + 1} < p_{i + 2}$，都可以将 $p_i, p_{i + 1}, p_{i + 2}$ 替换成一段 $p_i$ 到 $p_{i + 2}$ 的编号单调递增的路径，因此相邻两个点之间一定有边，引理得证。

用 $mn(x)$ 表示 $x$ 所在等价类的最小值，现在我们只需要证明对于任意满足以下条件的 $i, j, u, v$：

• $(i, u), (j, v) \in E_1$。
• $u, v$ 在同一等价类内。
• $mn(i) < mn(u), mn(j) < mn(u)$。

都满足 $i$ 所在等价类与 $j$ 所在等价类之间有边。

考虑此时有两个回文串，对于其中任意一个，不妨设其是 $s_{[a + 1, b - 1]}$，其中 $a = \min(i, u), b = \max(i, u)$，取出 $b$ 所在等价类中比 $b$ 小的最大的点 $c$，有回文串 $s_{[c, b]}$，分讨 $a$ 与 $c$ 的大小情况：

• 若 $c < a$，则 $c + b - a$ 与 $a$ 属于同一等价类，令 $a \gets c + b - a, b \gets c$，限制不变。
• 若 $c > a$，则有回文串 $s_{[c + 1, b - 1]}$，因此也有回文串 $s_{[a + 1, a + b - c - 1]}$，且 $a + b - c$ 与 $b$ 属于同一等价类，令 $b \gets a + b - c$，限制不变。

重复以上操作直到无法操作，此时必然有 $u = mn(u), i < u$。

对于 $j, v$ 同理，操作结束后有 $v = mn(v), j < v$。

此时根据引理一，$i$ 所在等价类与 $j$ 所在等价类之间有边。

证毕。

例题 3：The 1st Universal Cup, Stage 1: Shenyang H. P-P-Palindrome

给出 $n$ 个字符串 $s_1, s_2, \ldots, s_n$，请你计算出双倍回文的数量。

我们定义双倍回文为形式 $PQ$，其中回文串 $P$ 和回文串 $Q$ 都是某个 $s_i$ 的子串（$P, Q$ 可以来自不同的 $s_i$），且 $PQ$ 是回文串。

当 $P$ 或者 $Q$ 本质不同时，我们认为组成的 $PQ$ 是不同的。

$1 \le n, \sum_{i = 1}^n |s_i| \le 10^6$。

TL: 3s, ML: 512MB.

先找性质。不妨设 $|P| < |Q|$，显然 $Q$ 中有一段后缀为 $P$，而 $Q$ 存在于 $n$ 个串中。因此只需要枚举较长串，然后枚举其所有回文后缀有多少个和他拼起来也是回文串就行了。其中真后缀会提供 $2$ 的贡献，本身提供 $1$ 的贡献。

然后考虑拼起来是回文串的限制，也就是要 $\mathrm{pre}(Q, |Q| - |P|)$ 也是回文串，即数有多少 $i$，满足 $\mathrm{pre}(Q, i), \mathrm{suf}(Q, i + 1)$ 均为回文串。根据回文 Border 理论，$\mathrm{pre}(Q, i), \mathrm{suf}(Q, i + 1)$ 均为 $Q$ 的 Border，因此 $i, |Q| - i$ 均为 $Q$ 的周期。根据弱周期引理，$\gcd(i, |Q| - i)$ 也是 $Q$ 的周期，因此它是 $Q$ 的整周期，因此所有满足条件的 $i$ 即为 $Q$ 的最小整周期的倍数。设 $Q$ 的最小整周期为 $p$，则答案为 $2 \cdot \frac{|Q|}{p} - 1$。

对于 $n = 1$ 的情况，建出 PAM 就做完了，对于 $n > 1$ 的情况，可以将所有串拼在一起，并在相邻两个串之间添加两个不同的特殊字符连成一个串再建 PAM。

例题 4：洛谷 P5433 月宫的符卡序列

给一个字符串 $S$，下标从 $0$ 开始标号。

对于一个字符串 $T$，$T$ 的价值定义为，$T$ 在 $S$ 中所有出现位置的中点的异或。

中点的定义为，如果 $T=S[l \ldots r]$，则中点为 $\lfloor\frac{l+r}{2}\rfloor$。

求 $S$ 的所有回文子串的最大价值。

$t$ 组数据。

$1 \le |S| \le 10^6, 1 \le t \le 5$。

TL: 1s, ML: 125MB.

由于 PAM 的形式与后缀树类似，其也具有与后缀树类似的性质：每个节点对应的回文串的出现位置（$\mathrm{endpos}$）是其在 fail 树上所有后代的位置的并的超集。而其中心则是回文树上所有后代的位置的并的超集。

因此我们只需对每个极长回文子串维护其出现位置及对应在 PAM 上的节点即可。

求极长回文子串需要 Manacher，然后考虑怎么维护这个串在 PAM 上的位置，哈希一下就好了。

后缀自动机（Suffix Automaton, SAM）

endpos

讲后缀自动机之前首先要讲一下 $\mathrm{endpos}$。

对于字符串 $s$ 的任意非空子串 $t$，我们定义 $\mathrm{endpos}(t)$ 为 $s$ 中所有 $t$ 出现的位置的最后一个字符的位置，即：$\mathrm{endpos}(t) = \left\{x \mid s_{x - \left|t\right| + 1, x} = t\right\}$。

我们会发现对于某些子串可能会出现 $\mathrm{endpos}$ 相同的情况。
我们定义所有 $\mathrm{endpos}$ 相同的子串组成的集合为一个等价类。

性质 1：一个等价类里的所有子串一定是其中最长的子串的连续的后缀。

原因显然。

我们定义一个等价类中最长的子串为该等价类的代表元。

性质 2：一个等价类中的子串 $t$，其每次出现都是以代表元的后缀的形式。

显然。

性质 3：对于任意两个非空子串 $u, v (\left|u\right| \le \left|v\right|)$，一定满足 $\mathrm{endpos}(v) \subseteq \mathrm{endpos}(u)$ 或 $\mathrm{endpos}(u) \cap \mathrm{endpos}(v) = \varnothing$。

因为若 $\mathrm{endpos}(u)$ 与 $\mathrm{endpos}(v)$ 有交，则必然满足 $u$ 是 $v$ 的后缀。

为了方便叙述，下文中用 $\mathrm{len}$ 表示一个等价类中代表元的长度。
另外，为了方便理解，不妨定义 $\mathrm{endpos}(\text{空串}) = \varnothing$，且空串自己组成一个虚拟的等价类。

link

我们定义一个等价类的 $\mathrm{link}$ 为 $\mathrm{len}$ 最长的 代表元是 该等价类代表元后缀 的等价类。若不存在这样的等价类，则认为其 $\mathrm{link}$ 为空串的等价类。
注意，空串的等价类是为了方便理解我自己定义的，所以其没有 $\mathrm{link}$。

性质 1：如果将等价类视为一个点，每个等价类的 $\mathrm{link}$ 视为边，则其构成一棵内向树。

原因显然：每个点只有一个出边，且最终都指向虚拟等价类，且虚拟等价类没有出边。

我们称之为后缀链接树，或 parent tree。

性质 2：每个等价类的 $\mathrm{endpos}$ 一定是其儿子等价类的 $\mathrm{endpos}$ 的并集的超集（根除外），并且当且仅当其代表元为 $s$ 的前缀时会多一个元素，其他情况下相等。

每个等价类的元素一定是该等价类的儿子的元素的后缀。且对于任意非前缀的子串，其每次出现一定会对应某个以其为后缀的子串出现。

定义

终于要来力！

SAM 是一个接受 $s$ 的所有后缀的最小的 DFA。
SAM 的状态集合为所有等价类，起始状态为空串的等价类，接受状态为 $s$ 所有后缀所在的等价类。
SAM 的转移 $\delta(p, c)$ 的定义为，在 $p$ 中每个子串后添加一个字符 $c$ 得到的所有字符串所在的等价类。这些新的子串的 $\mathrm{endpos}$ 一定相同，关于这一点的正确性可以通过后文的 SAM 的构建来理解。

在所有满足上述条件的自动机中，SAM 是最小的。

性质 1：从起始状态出发，到达某一状态，按顺序记录下经过的转移的字符，其构成 $s$ 的一个子串。反之，$s$ 的每一个子串也对应某条路径。

性质 2：从起始状态出发到达某一状态的所有路径构成的字符串就是该等价类中的字符串。

构建

以下文字直接读可能有点难以理解，建议配合画 SAM 工具理解。
如果你突然读不懂了或者感觉哪里不是很显然，不妨回去看看 $\mathrm{endpos}$ 和 $\mathrm{link}$ 的定义及性质。

SAM 的构建是在线的。

假设我们已经构建好了 $\mathrm{pre}(s, i - 1)$ 的 SAM，要构建 $\mathrm{pre}(s, i)$ 的 SAM。

不妨令 $c = s_i$。

显然添加进 $c$ 后会出现一个新的等价类，其中仅有 $\mathrm{pre}(s, i)$，设其为 $u$，设 $\mathrm{pre}(s, i -1)$ 所在的状态为 $last$，显然有 $\mathrm{len}(u) = \mathrm{len}(last) + 1$。

考虑添加进 $c$ 后哪些状态会受到影响，发现只可能是原串（$\mathrm{pre}(s, i - 1)$）的后缀所在的等价类。我们可以通过从 $last$ 所在的状态跳 $\mathrm{link}$ 得到。

设我们当前跳到的状态为 $p$，我们讨论一下 $\delta(p, c)$ 的情况。

若 $\delta(p, c) = \mathrm{null}$，则说明之前没有出现过这些串，那么 $p$ 本身不受到影响，根据转移的定义，有 $\delta(p, c) = u$。
若一直往上跳直到跳到根都满足 $\delta(p, c) = \mathrm{null}$，说明此时 $\mathrm{pre}(s, i)$ 的所有后缀都在等价类 $u$ 中，故有 $\mathrm{link}(u) = start$。

否则，我们设 $q = \delta(p, c)$，若有 $\mathrm{len}(q) = \mathrm{len}(p) + 1$，则说明 $q$ 的代表元就是 $p$ 的代表元后面加上 $c$。$q$ 本身不受到影响，且根据 $\mathrm{link}$ 的定义，有 $\mathrm{link}(u) = q$。
若存在这种情况，我们发现 $u$ 不会对后面其他串产生影响，所以此时已经完成了对 $\mathrm{pre}(s, i)$ 的 SAM 的构建。

若 $\mathrm{len}(q) > \mathrm{len}(p) + 1$，我们发现以 $s_{i - \mathrm{len}(p), i}$，以及 $q$ 中其他比 $s_{i - \mathrm{len}(p), i}$ 短的字符串的 $\mathrm{endpos}$ 都添加了一个元素 $i$，而另一部分则没有变化。于是状态 $q$ 就被分裂开来了。我们不妨令 $\mathrm{endpos}$ 更新了的那部分被分裂出来，设其为 $v$。则：

• $\mathrm{len}(v) = \mathrm{len}(p) + 1$。
• 原先 $q$ 的所有转移也是现在分裂后的两个状态的转移，可以由定义得到。
• $\mathrm{link}(q) = v$，$\mathrm{link}(v)$ 则为原本 $q$ 的 $\mathrm{link}$，且 $\mathrm{link}(u) = v$。可以由 $\mathrm{link}$ 的定义得到。
• 对于所有指向原先 $q$ 的转移，代表元小于 $\mathrm{len}(v)$ 的转移指向 $v$，另一部分指向新的 $q$。

其他几个都很好处理，我们来考虑一下指向 $v$ 的转移。
我们发现被更新的转移的等价类一定在后缀连接树上是 $v$ 的祖先（由定义得到），于是只要从 $p$ 开始继续跳 $\mathrm{link}$，将所有指向 $q$ 的转移改成指向 $v$ 即可。
用与上面第二种情况类似的分析可以得到，若跳到的某个状态的 $c$ 的转移不是 $q$，则之后的状态的 $c$ 的转移也一定不是 $q$。

一些性质及证明

SAM 的状态数上限

SAM 的状态数上限为 $2n - 1$。
我们考虑构建 SAM 的过程，发现每次添加一个字符至多会多出两个状态。另外，不难发现添加前 $2$ 个字符时一定只会多出一个状态。加上初始状态，总状态数上限为 $1 + 1 + 1 + 2 \times (n - 2) = 2n - 1$。

SAM 的转移数上限

SAM 的转移数上限为 $3n - 4$。
我们考虑抠出任意一棵以初始状态为根的生成树。显然生成树上的边数上限为 $2n - 2$。
对于任意一个 $s$ 的后缀，我们记录其在 SAM 上转移时经过的第一条非树边。
考虑任意一条非树边 $(u, v)$，一定存在一条从初始状态到 $u$ 的只经过树边的路径，且一定存在一条从 $v$ 到接受状态的路径。
也就是说，任意一条非树边一定时某个后缀在 SAM 上转移时经过的第一条非树边。故非树边数量上限为后缀的数量。
显然一定有一种扣生成树的方式使得前两个后缀的转移不经过非树边。故转移数上限为 $2n - 2 + n - 2 = 3n - 4$。

构建 SAM 的时间复杂度

我们考虑构建 SAM 时的三种情况。
第二种情况的时间复杂度显然是 $O(\left|s\right|)$。
第一种情况可以视为在 SAM 中填加转移，故复杂度与转移数同为 $O(\left|s\right|)$。
第三种情况则可以视为遍历指向某个状态的转移，时间复杂度也是 $O(\left|s\right|)$。
故总时间复杂度为 $O(\left|s\right|)$。

注意实际应用中为了实现方便在第三种情况复制转移时一般会直接枚举所有 $\left|\Sigma\right|$ 种转移，这样时间复杂度会变成 $O(\left|s\right| \left|\Sigma\right|)$。

另外，对于字符集很大的情况，可以使用 map 来实现，时间复杂度变为 $O(\left|s\right| \log \left|\Sigma\right|)$

代码实现

struct SAM {
	int tot, lst;
	int len[2000005], link[2000005];
	int delta[2000005][26];

	SAM() {link[0] = -1;}
	void insert(char ch) {
		int c = ch - 'a', now = ++tot;
		len[now] = len[lst] + 1;
		for (int p = lst; p != -1; p = link[p])
			if (!delta[p][c]) delta[p][c] = tot;
			else if (len[delta[p][c]] == len[p] + 1) {link[now] = delta[p][c]; break;}
			else {
				int q = delta[p][c], v = ++tot;
				len[v] = len[p] + 1;
				memcpy(delta[v], delta[q], sizeof(delta[v]));
				link[v] = link[q], link[q] = v, link[now] = v;
				for (int i = p; delta[i][c] == q; i = link[i]) delta[i][c] = v;
				break;
			}
		lst = now;
		return ;
	}
} sam;

应用

求子串出现次数

相当于求其 $\mathrm{endpos}$ 的大小。
根据 $\mathrm{link}$ 的性质 2，只要在 $\mathrm{link}$ 树上 DP 即可。
另一种实现是，将所有状态按 $\mathrm{len}$ 排序后从大到小将其贡献加给父亲，本质上也是树形 DP。

例题：洛谷 P3804【模板】后缀自动机（SAM）。

求本质不同子串个数

答案为每个等价类的大小，即：

$$\sum\limits_u \mathrm{len}(u) - \mathrm{len}(\mathrm{link}(u))$$

同样的方法也能求本质不同子串长度之和，即：

$$\sum\limits_u \dfrac{\mathrm{len}(u) \times (\mathrm{len}(u) + 1)}{2} - \dfrac{\mathrm{len}(\mathrm{link}(u)) \times (\mathrm{len}(\mathrm{link}(u)) + 1)}{2}$$

例题：SDOI2016 生成魔咒。

求字典序第 k 小子串

等价于在给每条边按边权排序后的第 $k$ 小路径，拓扑排序求出每个状态的路径数即可。时间复杂度为 $O(ans \times \left|\Sigma\right|)$。

注意当 $k = 1$ 时，可以贪心走最小的边。
由此我们也可以得到求最小表示法的方法：将字符串复制一遍接在后面，然后在 SAM 上贪心走最小边。

例题：TJOI2015 弦论。

求子串第一次出现的位置

不妨设要求的是第一次出现的结尾所在的位置。

我们考虑构建 SAM 的过程。
每个状态的第一次出现的位置一定是在该状态被创建时确定的。
当创建 $\mathrm{pre}(s, i)$ 的状态时，其答案为 $i$。
当复制结点时，$v$ 的答案为 $q$ 的答案。

求子串的 endpos

我们加强一下 $\mathrm{link}$ 的性质 2。

我们发现某个串的每次出现都对应一个以它为后缀的 $s$ 的前缀的第一次出现，所以求一下每个串第一次出现的位置，然后在后缀链接树上 dfs 即可。

求最短未出现串

一个串没有出现等价于其在 SAM 上最终转移到 $\mathrm{null}$。要求最短，一定是最后一步转移到 $\mathrm{null}$。直接在 SAM 倒过来 DP 即可。

求两个串的最长公共子串

设这两个串分别为 $s$ 和 $t$。

我们对 $s$ 建立 SAM，然后用 $t$ 的每个前缀去匹配最长的后缀。

具体来说，假设当前在状态 $u$，匹配到了 $\mathrm{pre}(t, i)$，答案为 $l$。如果 $u$ 有 $t _ {i + 1}$ 的转移，则直接转移，并且 $l \gets l + 1$。

否则，我们就要缩小当前匹配的串。我们发现状态 $u$ 内的所有串都不可能成为答案，所以直接 $u \gets \mathrm{link}(u)$，直到 $u = start$ 或 $\delta(u, t _ {i + 1}) \neq \mathrm{null}$。

每次操作至多使 $l$ 增加 $1$，所以是线性的。

求多个串的最长公共子串

对于最短的串建 SAM，然后用其他串在上面跑两个串的算法，每次跑完对于每个状态取个历史最小值，然后再用后缀链接树上的儿子更新答案，即如果儿子有值则将该状态的答案设为 $\mathrm{len}$。

例题：SPOJ LCS2 - Longest Common Substring II。